Capítulo 2: Funções trigonométricas hiperbólicas
Este capítulo é dedicado ao estudo das funções trigonométricas hiperbólicas. Iremos primeiramente estudar algumas propriedades importantes das hipérboles, para que possamos deduzir algumas relações envolvendo esta trigonometria. Vamos, depois, definir as seis funções trigonométricas hiperbólicas e um pequeno estudo sobre cada uma delas, principalmente no que diz respeito a derivada de tais funções. Feito isto, vamos estabelecer as funções trigonométricas hiperbólicas inversas e concluímos o capítulo com o estudo das derivadas das funções inversas.
2.1 Propriedades da hipérbole
Consideremos uma hipérbole de equação
, para
. Para simplificar, vamos considerar que
e
são ambos
positivos, isto é, estamos tomando apenas um ramo da hipérbole. Os pontos desta curva são da forma
para
e o gráfico é a curva da figura
2.1
.
Dado um número real
, vamos considerar a transformação
Esta transformação é conhecida como deslocamento ou deslizamento sobre a hipérbole. Isto se deve ao fato de que
leva pontos da hipérbole na hipérbole (ver proposição
2.1
). Esta transformação é bastante importante no
nosso estudo e possui propriedades interessantes. As próximas proposições evidenciam algumas destas propriedades.
Outras propriedades podem ser encontradas em [
7
, Shervatov].
|
|
|
|
|
|
||
|
|
Se
é outro segmento desta reta com
e
, então da
mesma forma, o comprimento do segmento
é igual a
e a razão entre os
segmentos é
Vamos então provar que se
,
,
e
, então
. De fato,
,
,
e
. Então
|
|
|
|
|
|
||
|
|
e da mesma forma
e, portanto,
e isso prova o item
.
Para provar
, tomemos duas retas paralelas
e
, isto é, os coeficientes são proporcionais. Tomemos
as parametrizações
e
, para
. Então,
e
e, claramente,
e
são paralelas, já que os seus coeficientes são proporcionais.
Finalmente vamos a
. As assíntotas da hipérbole são os eixos coordenados. As suas parametrizações são
e
. Obviamente
, que continua sendo o eixo
e
, que continua sendo o eixo
.
Nota
: Observe que, na transformação dada em (
2.1
), para
temos a aplicação identidade. Para
, um dado ponto
será deslocado por
no sentido do crescimento do eixo
. E se
, então o
deslocamento de um determinado ponto
da hipérbole, se dará no sentido contrário ao do crescimento do eixo
.
Sabemos da geometria plana que a transformação
altera a área de uma figura plana multiplicando esta área por
e a segunda transformação multiplica a área de uma figura por
. A composta das duas
aplicações então multiplica a área de figuras primeiro por
e depois por
e, portanto, não
altera a área de figuras planas.
A figura
2.2
representa um braço da hipérbole de equação cartesiana
. Esta “metade”
de hipérbole é conhecida como hipérbole trigonométrica.
Note que, se rotacionarmos o gráfico da figura
2.2
,
no sentido anti-horário com relação a
origem, este braço de hipérbole se torna o braço de hipérbole da figura
2.1
, bastando apenas ajustar o valor
de
. Também as assíntotas
, após esta rotação, se tornam os eixos coordenados da figura
2.1
.
Isso significa que, por uma rotação, as propriedades listadas nas Proposições
2.1
e
2.2
são
válidas também na hipérbole trigonométrica e suas assíntotas
. Isto porque a rotação (de
), é
um movimento rígido e preserva comprimento de segmentos, relação de paralelismo e medidas de áreas.
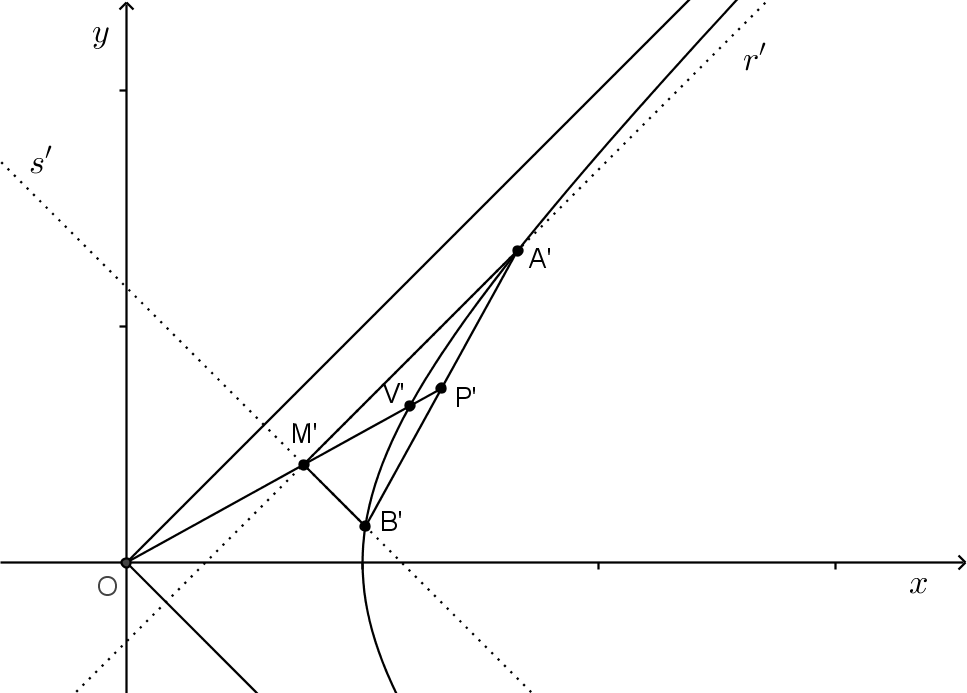
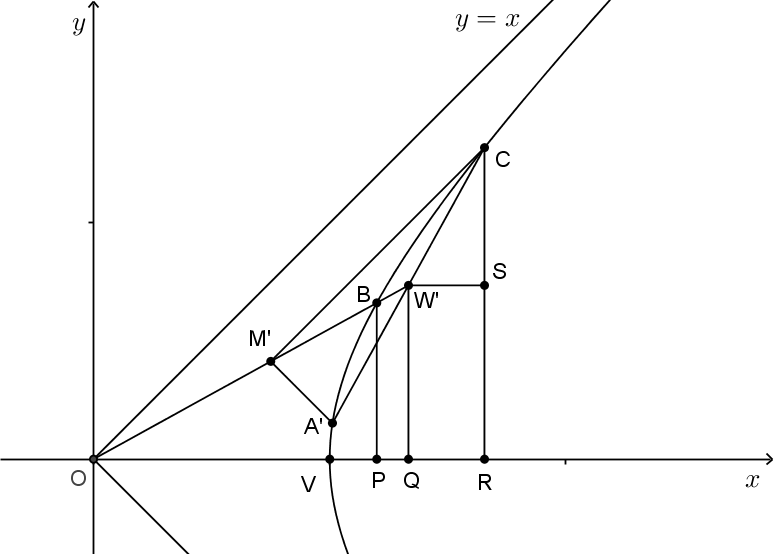
Chamemos
o vértice da hipérbole da figura
2.2
. Consideremos um ponto
sobre a hipérbole
situado no primeiro quadrante (fig.
2.3
). Pelo ponto
traçamos a perpendicular
ao eixo
. Marcamos
o ponto
simétrico de
com relação ao eixo
. O segmento
é dito segmento conjugado do segmento
, pois
o prolongamento de
encontra
no ponto médio
de
. O ponto
está então sobre a hipérbole no quarto
quadrante e o segmento
é também perpendicular ao eixo
. Traçamos pelo ponto
a reta
paralela a assíntota
e pelo ponto
a reta
paralela a assíntota
. As retas
e
se encontram no ponto
, sobre o
eixo
, formando o triângulo
retângulo em
.
Aplicamos agora um deslizamento sobre a hipérbole, isto é, aplicamos a transformação
dada em (
2.1
).
Obtemos assim os pontos
,
,
,
e
imagem pela
dos pontos
,
,
,
e
respectivamente; e as retas
e
imagem pela
das retas
e
respectivamente, conforme figura
2.4
.
Nestes termos, como os pontos
,
e
estão sobre uma mesma reta, pela propriedade
da Proposição
2.1
os pontos
,
e
estão também sobre uma mesma reta. Pela mesma razão, os pontos
,
,
e
também estão alinhados, isto é, sobre uma reta. Os pontos
,
e
ainda estão sobre a hipérbole.
A razão entre as medidas dos segmentos
e
é igual 1 e, portanto, pelo item
da Proposição
2.1
, a razão entre as medidas dos segmentos
e
é também 1, isto é, o ponto
é ainda o ponto
médio do segmento
. Pelas propriedades
e
da mesma Proposição, as retas
e
são paralelas as retas imagens das assíntotas
por
. Como as assíntotas não são alteradas,
e
ainda são paralelas as assíntotas. Isto significa que o triângulo
é ainda um triângulo retângulo em
.
2.2 A trigonometria hiperbólica
A trigonometria hiperbólica é construída sobre a hipérbole trigonométrica, isto é, o braço da hipérbole de equação
, representado na figura
2.2
. Dado um número real
, entenderemos por ângulo
hiperbólico
, ou ângulo hiperbólico
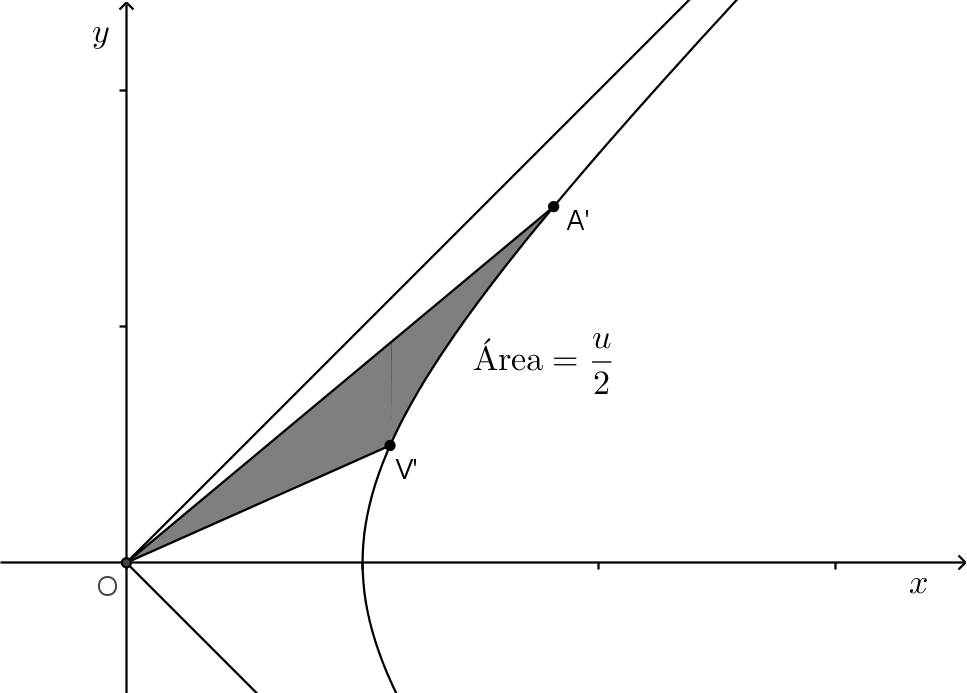
, o arco
da hipérbole no primeiro quadrante, de forma que a área do
setor
seja igual a
(Ver figura
2.5
). No caso em que
o ângulo hiperbólico
é o arco
da hipérbole, no quarto quadrante, de forma que a área do setor
seja igual a
.
Note que esta definição, em termos de área, é escolhida pois o deslizamento hiperbólico não altera área de figuras
no plano (Proposição
2.2
) e desta forma um ângulo hiperbólico
não será alterado quando aplicarmos o
deslizamento hiperbólico. Na figura
2.6
, o ângulo hiperbólico
é igual ao ângulo hiperbólico
se
e
são imagens respectivas dos pontos
e
por deslizamento hiperbólico.
Note ainda que podemos considerar ângulos hiperbólicos de qualquer magnitude, já que a área do setor entre as
assíntotas
e a hipérbole, é infinita. Vamos agora definir seno e cosseno hiperbólico de um ângulo
(hiperbólico)
.
Nesses termos, dado um ângulo hiperbólico
, determinado pelo arco de hipérbole
, consideramos o ponto
,
projeção do ponto
sobre o eixo
e o ponto
projeção do ponto
sobre o eixo
. O cosseno hiperbólico de
é definido como sendo a abscissa do ponto
, isto é, o comprimento do segmento
orientado
(ou
), com relação ao eixo
. Note que este segmento orientado nunca terá sentido contrário ao
eixo
e, portanto, a medida de cosseno hiperbólico de
será sempre positiva (maior ou igual a 1 para ser mais
preciso). O seno hiperbólico de
é definido como sendo a ordenada do ponto
, isto é, o
comprimento do segmento orientado
(ou
), com relação ao eixo
, isto é, se o segmento orientado
tem
sentido contrário ao eixo
, então entendemos que a medida do segmento é negativa. Isto ocorrerá apenas para valores
negativos de
.
Representamos isto escrevendo
As demais funções trigonométricas hiperbólicas, tangente, cotangente, secante e cossecante, são definidas como na trigonometria circular, isto é, respectivamente
|
|
|
|
|
|
e
|
Se considerarmos dois ângulos hiperbólicos de medidas
e
, representados respectivamente pelos arcos
e
, vemos (na figura
2.8
) que os valores de seno hiperbólico são diferentes apenas por um sinal, pois os
segmentos orientados
e
tem sentidos opostos e que os valores de cosseno hiperbólico são ambos iguais ao
segmento orientado
.
Isto significa que,
Em outras palavras, o seno hiperbólico é uma função ímpar e o cosseno hiperbólico é uma função par.
Nosso próximo passo é deduzir as principais fórmulas da trigonometria hiperbólica. Serão cinco fórmulas, contando com as duas identidades em ( 2.2 ). Faltam a relação fundamental e as fórmulas de soma de arcos para o seno e o cosseno hiperbólicos. Demais fórmulas trigonométricas que se deseje podem ser deduzidas a partir destas cinco.
Da figura
2.7
, podemos ver claramente que as coordenadas cartesianas do ponto
são
. Também o ponto
está sobre a hipérbole, e então suas coordenadas devem obrigatoriamente satisfazer a
equação da hipérbole
e, assim,
que é a relação fundamental da trigonometria hiperbólica.
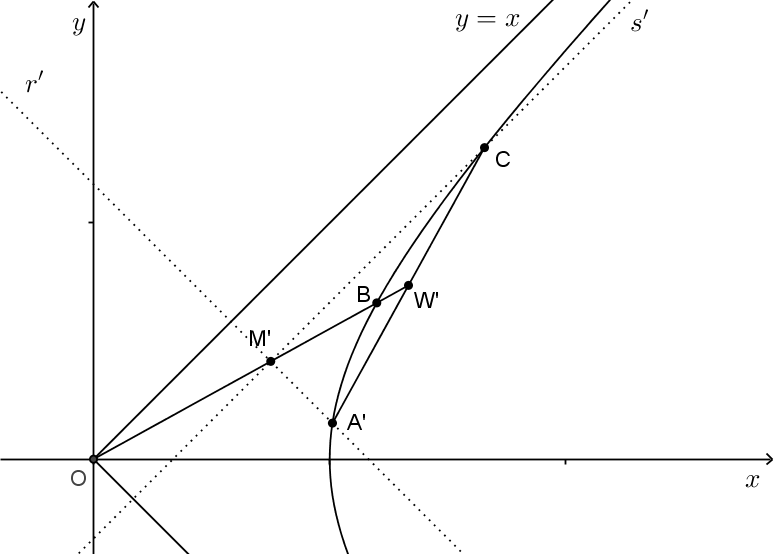
Vamos agora mostrar a validade das fórmulas trigonométricas da soma de arcos do cosseno hiperbólico e do seno
hiperbólico. Consideremos dois ângulos hiperbólicos
e
determinados pelos arcos hiperbólicos
e
respectivamente, conforme a figura abaixo.
Tomando o ponto
, sobre a hipérbole, simétrico do ponto
pelo eixo
, temos o segmento
conjugado ao
segmento
, isto é, o prolongamento do segmento
corta o segmento
em seu ponto médio. Chamemos
, este
ponto médio.
também é a projeção de
sobre o eixo
. Considerando as retas
e
paralelas as assíntotas
, que passam pelos pontos
e
respectivamente, temos que
e
se encontram sobre o eixo
no
ponto que denotaremos por
.
Decorre disto que
Vamos agora aplicar um deslizamento hiperbólico que desliza o arco
de forma que a imagem
de
coincide com
o ponto
. A imagem de
então será denotada por
, isto é,
. Lembrando ainda que o ângulo hiperbólico
continua sendo o ângulo hiperbólico
, em virtude da invariância de áreas por deslizamento hiperbólico. O ponto
por sua vez determina o arco de hipérbole
associado ao ângulo hiperbólico
. Também, sejam
,
e
as respectivas imagens dos pontos
,
e
e
e
as respectivas imagens das retas
e
.
Pelos pontos
e
traçamos, as perpendiculares ao eixo
,
e
. Lembremos que a corda
, é ainda
conjugada a
, ou seja, o prolongamento de
encontra o ponto médio do segmento
e com
sendo este
ponto médio.
Nestes termos temos as relações,
e
Vamos agora mostrar que também valem,
Os segmentos
e
estão sobre a mesma reta e então do item
da proposição
2.1
temos que
a razão
é preservada pelo deslizamento hiperbólico, ou seja,
. Levando
em conta que
, temos imediatamente que
Agora, os triângulos
e
são triângulos retângulos e
e
são pontos médios das respectivas
hipotenusas. O ponto médio da hipotenusa é equidistante aos vértices de um triângulo retângulo, isto é,
e
. Também, como os segmentos
e
estão sobre uma mesma reta, a razão
é
preservada pelo deslizamento hiperbólico, isto é,
. Segue que
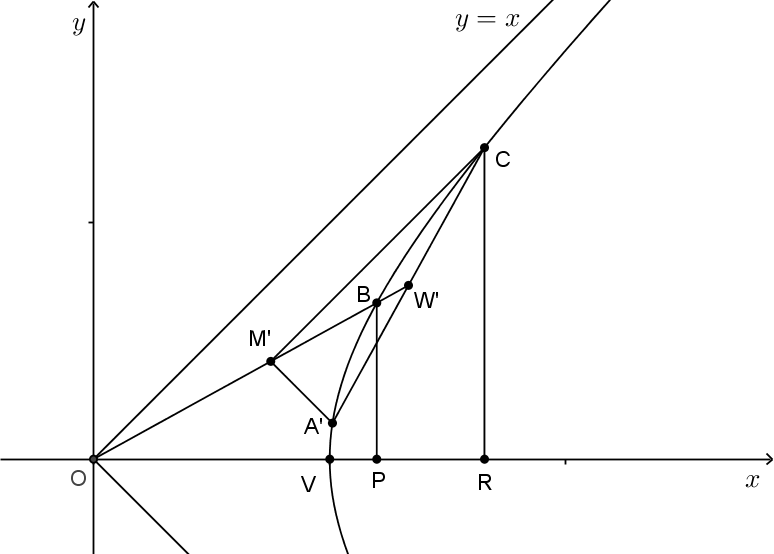
Seja
a projeção de
sobre o eixo
e
a projeção de
sobre o segmento
, conforme a figura
2.13
.
Notemos que os triângulos
e
são semelhantes. Vamos verificar que também são semelhantes os triângulos
e
. Para isto mostraremos que o ângulo
é igual ao ângulo
. A reta
, paralela a
bissetriz
, passa por
, intercepta
em
e intercepta
em um ponto que chamaremos de
(Figura
2.14
).
Assim,
. Mais ainda, como o triângulo
é retângulo em
e
é o ponto
médio da hipotenusa
, segue que o triângulo
é isósceles e pontanto os ângulos
e
possuem a mesma medida, isto é,
. Mas
e, portanto,
.
Segue disto que
Agora,
e, portanto,
e como
então temos,
como desejado. Isto mostra que os triângulos
e
são semelhantes. Desta semelhança, segue que
e destas igualdades,
Também são semelhantes os triângulos
e
e desta semelhança, temos
e destas igualdades,
Finalmente, lembrando que
temos,
e também,
As fórmulas ( 2.5 ) e ( 2.6 ), juntamente com a relação fundamental ( 2.3 ) e as duas fórmulas em ( 2.2 ), constituem as 5 fórmulas básicas da trigonometria hiperbólica. Com elas podemos deduzir outras fórmulas, como por exemplo, as fórmulas de duplicação de arcos,
|
|
|
|
|
|
||
|
|
|
|
|
|
e as fórmulas de diferença de arcos,
|
|
|
|
|
|
||
|
|
|
|
|
|
Vamos agora obter duas outras fórmulas trigonométricas hiperbólicas que serão úteis mais adiante. São fórmulas fáceis de serem obtidas, similares às fórmulas obtidas na proposição 1.1 . Estamos apresentando-as em virtude do uso futuro (na seção 2.8 ).
|
|
Para todos
|
|
|
Para todo
|
|
|
Para todo
|
|
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
|
|
Os itens
e
ficam
|
|
|
|
|
|
||
|
|
||
|
|
e
|
|
|
|
|
|
||
|
|
||
|
|
e a prova está concluída.
2.3 As funções trigonométricas hiperbólicas
Nesta seção, vamos estudar os aspectos das funções trigonométricas hiperbólicas. Primeiro vamos observar os gráficos dessas funções, determinando, com precisão, os respectivos domínios. Também, vamos observar alguns limites importantes em cada uma das funções. Para esse nosso estudo, vamos considerar as funções de uma variável real
que a cada valor de
associa o seno, ou o cosseno, ou a tangente, ou a cotangente, ou a secante, ou ainda a cossecante hiperbólica de
. Vamos olhar uma a uma.
Para a função
, notemos que para cada valor real de
, construímos o ângulo hiperbólico
determinado pelo arco
, onde a ordenada do ponto
é o seno hiperbólico de
.
Não há nenhuma impossibilidade matemática para
e, portanto, o domínio da função
é todo o conjunto
dos números reais. Além disso, fazendo
variar no conjunto dos reais, os valores resultantes para a ordenada do
ponto
também percorrem o conjunto dos números reais. Desta forma, temos que a função
|
|
|
|
|
|
|
|
|
é sobrejetiva. Além disso, para cada
Conforme
aumenta (para o infinito) o tamanho do arco
também aumenta. Por conseguinte, a ordenada do ponto
aumenta e o valor de
também aumenta indefinidamente. O mesmo ocorre para os valores negativos de
. Temos
então
O gráfico de
é dado por
Podemos notar ainda que é uma função contínua (mostraremos isto formalmente na próxima seção), ímpar e estritamente crescente.
Agora a função
.
Para qualquer valor real
, construímos o arco
hiperbólico
associado ao ângulo hiperbólico
, cujo cosseno hiperbólico é a abscissa do ponto
. Notemos que
não há nenhuma impossibilidade matemática para o valor de
e, sendo assim, o domínio da função
é o
conjunto dos números reais. Fazendo
variar no conjunto dos números reais, vemos que a abscissa do ponto
somente
poderá assumir valores maiores do que
, isto é,
. Isto significa que esta função não é
sobrejetora no conjunto dos números reais, mas sim no conjunto
. Note também que esta função não é
injetora, pois para qualquer valor de
temos
, isto é, é uma função par. Portanto a função
|
|
|
|
|
|
|
|
|
não é bijetora.
Conforme o valor de
aumenta (para o infinito), o tamanho do arco
aumenta e a abscissa do ponto
também
aumenta indefinidamente. Uma análise similar para valores negativos de
levam à mesma conclusão. Temos assim,
O gráfico desta função é dado por
Para a função
vamos usar a identidade
.
Fazendo
variar no conjunto dos números reais, temos apenas que nos preocupar com o denominador,
que não pode ser nulo. Como vimos anteriormente, para qualquer valor de
, temos que
é maior ou igual a 1,
e, portanto, o denominador da fração anterior, não se anula. Com isto o domínio da função
é todo o
conjunto dos números reais.
Além disso, como o ponto
está entre as retas assíntotas
e
, temos que a abscissa do ponto
é
sempre maior que a ordenada do ponto
em módulo, isto é,
para qualquer valor de
. Isto
significa que a fração
resultará sempre valores menores que 1 em módulo, isto é,
.
À medida que
aumenta indefinidamente, os valores de
e
tendem a se igualar, pois o ponto
se
aproxima da assíntota
e isto significa que quando
os valores de
se aproximam de 1. No
caso em que
então o ponto
se aproxima da assíntota
e neste caso levamos em conta os sinais
de
e
. Em outras palavras,
O gráfico da função
é dado por
A função
é uma função monótona crescente, ímpar, limitada e bijetora de
em
.
O estudo da função cotangente hiperbólica,
, também será feito analizando a identidade
.
Para determinar o domínio desta função, como se trata de
um quociente, precisamos nos preocupar com o anulamento do denominador. O seno hiperbólico se anula somente no ponto
e, portanto, o domínio de
é o conjunto
.
Também, como visto anteriormente, o numerador é sempre maior que o denominador, em módulo. Portanto os valores
resultantes deste quociente são sempre maiores que 1, em módulo, isto é, a imagem desta função é o conjunto
. À medida que
cresce indefinidamente, os valores de
e
se aproximam (veja
explicação anterior) e, portanto,
Como o ponto
é um ponto crítico desta função, vamos estudar os limites no ponto 0. A medida que
se aproxima
de
0
, os valores do denomidador
, se aproximam de
0
e a fração vai para o infinito. Temos então, com o
respectivo estudo de sinal lateral,
O gráfico desta função é dado por
A função
é uma função ímpar e bijetora do conjunto
no conjunto
.
Para a função
,
o domínio é o conjunto dos
números reais, uma vez que o denominador nunca se anula, mais do que isto, o denominador é sempre maior ou igual a 1.
Portanto, os valores assumidos pelo quociente
, serão sempre positivos e menores ou iguais a
e,
desta forma, a função é limitada inferiormente por 0 e superiormente por 1. Além disso, como cosseno hiperbólico é uma
função par, então a função secante também será uma função par.
À medida que
cresce indefinidamente, o denominador também cresce indefinidamente e, portanto,
O gráfico desta função é
A cossecante hiperbólica é dada pelo quociente
e desta forma, seu domínio é o conjunto dos números reais tais que o denominador não se anula, isto
é,
. A imagem por sua vez é também o conjunto
já que a fração
jamais se anula.
Conforme
cresce (para o infinito), o denominador também cresce (para o infinito) e, assim,
Próximo do ponto crítico
os valores do denominador também estarão próximos de
0
e, portanto, fazendo o estudo
de sinal, temos
O gráfico da função cossecante hiperbólica é
A função cossecante hiperbólica é uma função ímpar bijetora de
em
. É decrescente em cada um dos
semi-eixos positivo e negativo.
A relação completa das funções trigonométricas hiperbólicas, com os domínios e imagens é resumida na próxima tabela.
2.4 Continuidade das funções trigonométricas hiperbólicas
Agora vamos mostrar que as funções trigonométricas hiperbólicas são contínuas em cada um dos pontos de definição destas funções. Mais precisamente, mostraremos que
para qualquer
.
Nestes termos, sabemos que a área do setor hiperbólico
(a área sombreada da figura (
2.5
)) é igual
a
, a área do triângulo
é igual a
e a área do triângulo retângulo
é igual
a
. Também a área do triângulo
é menor que a área do
setor hiperbólico
que por sua vez é menor que a área do triângulo
, ou seja,
Multiplicando tudo por 2 e dividindo tudo por
(que é positivo), temos
ou ainda,
Da primeira desigualdade temos que
e, usando isto, temos
|
|
|
|
|
|
||
|
|
Desta forma
e, reorganizando os termos, temos
e como
então
, o que nos permite obter
. Segue que
Passando agora o limite na desigualdade, quando
, temos que o limite do termo do lado esquerdo existe e é
igual a 1 e o limite do lado direito também existe e é igual a 1, pois
é uma função contínua em
. Temos então pelo teorema do confronto (teorema do sanduíche) que
O caso em que
, é obtido observando que a função
é uma função par. Assim o comportamento à
esquerda de 0 é o mesmo comportamento à direita de zero. Temos então
e, portanto,
o que encerra esta demonstração.
e o teorema do confronto garante que
. Para
lembremos que cosseno
hiperbólico é uma função par e então como na demonstração do teorema anterior,
e isso prova o primeiro limite.
Para provar o segundo limite, usaremos o item (c) do teorema
1.2
. Como os limites de
e de
existem quando
então o limite do produto existe e
Agora, como
para todo
então do teorema
1.4
segue que
e isso finaliza esta demonstração.
|
|
|
|
|
|
||
|
|
Usando agora a identidade trigonométrica para a soma de arcos do seno hiperbólico, temos
|
|
|
|
|
|
||
|
|
||
|
|
e isso termina esta demonstração.
Os limites indicados no início desta seção seguem agora imediatamente do teorema de mudança de variáveis 1.5 , e dos limites que acabamos de provar.
Vamos agora analisar a continuidade das outras quatro funções trigonométricas hiperbólicas, já que estas são escritas como um quociente em termos de seno e cosseno. Usando o item (d) do teorema 1.2 , podemos facilmente provar as afirmações a seguir.
As funções tangente, cotangente, secante e cossecante hiperbólicas são contínuas nos seus domínios de definição. Isto é,
|
|
|
|
|
|
|
|
|
|
|
2.5 Derivadas de funções trigonométricas hiperbólicas
Vamos agora deduzir as derivadas das funções trigonométricas hiperbólicas. Para isto usaremos primeiro a definição de derivada, isto é,
para encontrar as derivadas de
e
. Depois usaremos a regra do quociente para obter as derivadas das
demais funções trigonométricas hiperbólicas. Antes precisamos determinar um limite importante.
Usando agora a identidade fundamental ( 2.3 ) no membro da direita, temos que
Olhando para o membro da direira, temos que, o limite da primeira fração quando
existe e é igual a 1
(proposição
2.4
) e o limite da segunda fração quando
também existe por ser uma função contínua
em
. Desta forma o limite do produto existe quando
e,
|
|
|
|
|
|
e a prova está terminada.
Agora temos condições de deduzir as fórmulas de derivada para as funções trigonométricas seno e cosseno hiperbólicos. Para a função seno hiperbólico temos que a derivada é dada por,
em todos os valores
tais que o limite existe.
Assim,
|
|
|
|
|
|
||
|
|
para todo
tal que o limite acima existe.
Mas os limites de
e
existem para todo
e assim,
|
|
|
|
|
|
para todo
.
Para a função cosseno hiperbólico, temos que
para todo
tal que o limite exista. Para tais
, temos
|
|
|
|
|
|
||
|
|
Como os limites de cada uma das frações
e
existem para
todo
então
|
|
|
|
|
|
para todo
.
Para as demais funções trigonométricas hiperbólicas usaremos as identidades em termos de seno e cosseno hiperbólico e a
regra de derivação do quociente. Já que as funções seno e cosseno hiperólico são diferenciáveis em todo
então os quocientes de definição das demais funções trigonométricas hiperbólicas são diferenciáveis em todos os pontos
onde o denominador não se anula.
A função
é diferenciável em todo
e
|
|
|
|
|
|
Para a função cotangente, temos em todo
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A tabela abaixo, reúne as fórmulas de derivação para as funções trigonométricas hiperbólicas. O conjunto domínio descrito na tabela é o domínio da derivada. Note a semelhança com o caso circular.
2.6 Funções trigonométricas hiperbólicas inversas
Nesta seção, vamos definir as funções trigonométricas inversas, estabelecendo os domínios, as imagens e indicando alguns limites importantes. Também apresentaremos os gráficos destas funções. Este não é um trabalho muito fácil pois, como acabamos de ver, as funções trigonométricas hiperbólicas não são todas elas bijetoras. Já passamos por este problema na seção 1.5 com as funções trigonométricas circulares. Vamos impor, quando necessário, condições de restrição de domínio e de imagem para tornar as funções bijetivas.
Comecemos com a função seno hiperbólico, que como vimos anteriormente, é uma função bijetora de
em
. Desta
forma, podemos obter a função inversa do seno hiperbólico, para qualquer valor real. Dado
, o seno
hiperbólico inverso de
, é o número
, representado por
, que satisfaz
. É usual
representar também a função seno hiperbólico inverso por
e lemos “arco seno
hiperbólico”. Vamos usar neste texto a primeira notação e lembre-se de não confundir
com
. A segunda expressão é o inverso multiplicativo do seno hiperbólico, ou seja a cossecante hiperbólica.
Fazendo
variar em
, temos a função seno hiperbólico inverso,
|
|
|
|
|
|
|
|
|
que satisfaz a relação
. Se fizermos
tender para o infinito, a relação
nos diz que
também deve ir para o infinito e analogamente para
. Temos assim,
Valem as seguintes relações inversas,
|
|
||
|
|
O gráfico da função seno hiperbólico inverso, é da forma,
A função cosseno hiperbólico não é uma função bijetora. Lembremos que seu domínio é
, mas sua imagem é o
subconjunto
. Restringindo o contradomínio a
tornamos esta função sobrejetora.
Também a função cosseno hiperbólico, definida em todo o domínio
, não é injetora. Vamos então restringir o domínio
desta função ao conjunto dos reais não negativos. Temos assim que a função cosseno hiperbólico é bijetora de
em
. Por restrição, podemos então definir a função cosseno hiperbólico inverso, denotada por
|
|
|
|
|
|
|
|
|
e que satisfaz a relação
. Levando
ao infinito, a relação
nos mostra que
também vai
para o infinito. No outro extremo do intervalo de definição, isto é, quando
tende para 1 (somente pela direita), a
mesma relação mostra que
vai para 0. Então,
O gráfico desta função é a curva da figura abaixo.
Ocorrem as seguintes relações inversas,
|
|
||
|
|
A função tangente hiperbólica é uma função injetora do conjunto
no conjunto
, mas não é sobrejetora já que o
conjunto imagem é o intervalo
. Restringindo o contradomínio temos a bijetividade da função tangente
hiperbólica de
em
. Definimos então a função tangente hiperbólica inversa,
|
|
|
|
|
|
|
|
|
com
e
satisfazendo
. Vamos observar o seu comportamento nos extremos do intervalo. Quando
tende
a 1 (pela esquerda) então a relação
mostra que
deve ir para o infinito. Analogamente se
então
vai para
. Resumindo,
O gráfico da função tangente hiperbólica inversa,
As relações inversas são
|
|
||
|
|
A função cotangente hiperbólica também é uma função bijetora do conjunto
no conjunto
. Desta forma, definimos a função cotangente hiperbólica inversa por,
|
|
|
|
|
|
|
|
|
desde que
. Analisando os extremos do intervalo de definição, temos que quando
a relação
nos diz que isto ocorre quando
vai para 0 (com valores negativos). Analogamente, quando
então deve ocorrer
(com valores positivos). Fazendo
então, a mesma relação anterior,
nos diz que
deve ir para
e analogamente
quando
. Resumindo,
|
|
|
|
|
|
|
|
O gráfico desta função é dado por
Valem as seguintes relações de inversão,
|
|
||
|
|
Para a secante hiperbólica, temos alguns problemas como no caso do cosseno hiperbólico inverso. O domínio da
função secante hiperbólica é o conjunto
e a imagem é o conjunto
. Mas esta função não é injetora de
em
. Então vamos restringir o conjunto domínio para os reais não negativos. Assim, a função secante hiperbólica
é bijetiva de
em
e podemos definir a função secante hiperbólica inversa
|
|
|
|
|
|
|
|
|
satisfazendo
. Quando
(pela direita), a relação
diz que
deve estar indo para o infinito por valores positivos e consequentemente
deve estar indo para o infinito.
Quando
vai para 1 (pela esquerda) então
está indo para 1 e
deve estar se aproximando de 0. Temos
então
As relações inversas ficam,
|
|
||
|
|
Graficamente, temos
Finalmente, lembremos que a função cossecante hiperbólica é bijetora do conjunto
no conjunto
.
Definimos então a função cossecante hiperbólica inversa
|
|
|
|
|
|
|
|
|
que também satisfaz
. Esta relação explica também os limites. Quando
então
deve ir para 0 por valores negativos e então
deve ir para 0 também por valores negativos.
Analogamente, quando
,
deve ir para 0 por valores positivos e então
deve ir também para 0
por valores positivos. Se
por valores positivos então
deve ir para o infinito e
também. Da mesma forma, se
por valores negativos, então
vai para
e consequentemente,
também. Resumindo,
|
|
|
|
|
|
|
|
O gráfico desta função é representado por
São válidas as relações de inversão,
|
|
||
|
|
A relação completa de funções trigonométricas hiperbólicas inversas com seus respectivos domínios de definição e conjunto imagem é dada na próxima tabela.
2.7 Continuidade das funções trigonométricas hiperbólicas inversas
O procedimento adotado aqui não tem diferenças do procedimento adotado para as funções trigonométricas circulares. O teorema 1.11 se aplica às funções trigonométricas hiperbólicas em seus respectivos domínios de definição. Vamos omitir os detalhes. Entretanto entendemos deste ponto em diante que cada função trigonométrica inversa é contínua nos seus respectivos domínios de definição respeitando a lateralidade nos extremos fechados destes domínios.
Temos assim, que
|
|
para todo |
|
|
|
para todo |
|
|
|
para todo |
|
|
|
para todo |
|
|
|
para todo |
|
|
|
para todo |
|
2.8 Derivadas das funções trigonométricas hiperbólicas inversas
Nesta seção, vamos determinar as fórmulas de derivada para as funções trigonométricas hiperbólicas inversas. Usaremos principalmente a técnica da diferenciação implícita e levamos em conta o conhecimento das fórmulas de diferenciação para as seis funções trigonométricas hiperbólicas obtidas na seção 2.5 .
Considerando a função
, para todo
, queremos agora derivar em relação a
e obter
. Sabemos que neste caso é válida a relação
. Lembre-se que
é variável dependente
de
e, por isto, quando derivarmos
devemos usar diferenciação implícita. Nestes termos, derivando em relação a
os dois membros de
, temos
Como queremos determinar
basta agora isolar este termo. Obtemos
Mas claro que desejamos obter esta derivada como função de
novamente. Precisamos então substituir a variável
dependente
do segundo membro pela variável independente
. A única expressão que faz esta substituição é a
própria relação
. Assim, vamos substituir o termo
por alguma expressão que contenha
.
Usando a relação fundamental (
2.3
), temos
para todo
.
Tomamos agora a função
, definida para todo
. Derivando implicitamente a
igualdade
com relação a
, para todo
, obtemos
Isolando agora o termo
, como feito para o caso do seno hiperbólico e usando a relação fundamental
(
2.3
), obtemos
para todo
. Note que esta derivada não está definida para
.
Para a função
, definida no intervalo
, derivamos a igualdade
com relação
a
, obtendo
Reorganizando os termos e usando a igualdade ( 2.8 ), da proposição 2.3 , vem
para todo
.
Considerando
, definida para todo
, vamos derivar a
igualdade
com respeito a
. Obtemos
Isolando o termo
e usando a identidade (
2.9
) da proposição
2.3
,
temos
para
.
Tomando agora a função
, que está definida para todo
, temos
, com
. Derivando em relação a
, obtemos
para todo
. Então,
Usaremos a identidade (
2.8
) da proposição
2.3
, válida para
. Extraindo a
raiz quadrada em ambos os membros de (
2.8
), temos que
Como
o termo
do lado esquerdo é sempre positivo. Descartamos então o módulo, obtendo
Finalmente para a função
, definida para todo
, escrevemos
, com
e derivando implicitamente em relação a
, obtemos
que nos fornece
Vamos usar a igualdade (
2.9
), da proposição
2.3
, válida para
. Extraímos a
raiz quadrada em ambos os membros de (
2.9
) para obter
Observe que
não é sempre positiva para
e isto nos impede de descartar o módulo. Mas
é sempre positivo. Então temos
|
|
|
|
|
|
||
|
|
donde segue que
para todo
.
Vamos resumir as fórmulas desta seção na próxima tabela.
Note que as derivadas das funções
e
são iguais, porém estão definidas em conjuntos
disjuntos, isto é, conjuntos que não possuem pontos em comum.