Capítulo 4: Aplicações




Alguns alunos acreditam que as funções trigonométricas, principalmente as hiperbólicas, existem apenas para complicar suas vidas. Uma ferramenta a mais para o professor acabar com suas noites de sono tranquilo. Infelizmente para os alunos e felizmente para a matemática, essas funções não são descartáveis. Neste capítulo, apresentaremos algumas situações onde são utilizadas as funções trigonométricas.

Os livros de ensino fundamental e médio já apresentam algumas aplicações a respeito destas funções, tais como o cálculo da altura de obstáculos (torres, edifícios e montanhas), do raio da terra, da distância entre objetos, entre outras aplicações. São em geral situações onde podem ser utilizados argumentos geométricos com triângulos retângulos.

As aplicações que iremos aqui apresentar, são um pouco mais complexas e exigirão a utilização de trigonometria no contexto das funções. Para uma melhor compreensão destas aplicações recomendamos ao leitor algum conhecimento de cálculo diferencial e integral, geometria, equações diferenciais e de conceitos físicos. De qualquer forma, em cada seção tentaremos apresentar, mesmo que sem demonstração, alguns dos resultados ou conceitos que desejamos utilizar.

4.1 Cálculo do número \(\pi\)

O número “pi”, é conhecido da humanidade ainda antes de Cristo. É difícil dizer com precisão quando foi concebido, mas desde muito cedo, o homem percebeu que dividindo o comprimento de uma circunferência qualquer pelo seu diâmetro, resultava sempre um mesmo valor.

O símbolo atual que designa o número “pi” é a letra grega $\pi $, que foi utilizada pela primeira vez em 1706 por William Jones, mas só foi amplamente aceita quando usada por Euler em 1737. Fato este que não nos impedirá de usar a notação atual $\pi $, mesmo para citações mais antigas.

O primeiro matemático a investigar o número $\pi $ foi Arquimedes (287-212 a.C.). Ele efetivamente calculou uma aproximação para $\pi $. Arquimedes construiu polígonos regulares inscritos e circunscritos em uma circunferência e calculou o perímetro destes polígonos. Quanto mais lados ele colocava no polígono, melhor a aproximação. Usando um polígono regular de 96 lados, Arquimedes afirmou que

$\displaystyle 3 + \frac{10}{71} < \pi < 3 + \frac{10}{70}, $

ou seja, $\frac{223}{71} < \pi < \frac{22}{7}$. A fração $\frac{22}{7}$ é uma das mais famosas aproximações para $\pi $. Entretanto, um artifício do Cálculo Diferencial e Integral nos mostra que $\pi \neq \frac{22}{7}$. Mais precisamente,

$\displaystyle 0 < \int_{0}^{1} \frac{x^4(1-x)^4}{1+x^2} dx = \frac{22}{7}-\pi. $

Arquimedes, assim como outros matemáticos de sua época, acreditava que $\pi $ fosse um número racional. No entanto, em 1761 o alemão Johann Lambert provou que $\pi $ é um número irracional. Isto significa que esse número, assim como todos os números irracionais, possui infinitas casas decimais que não apresentam comportamento periódico.

Devido a este fato, vários matemáticos ficaram ocupados durante algum tempo para calcular o valor de $\pi $ com mais casas decimais corretas. O objetivo desta seção é mostrar como a função arco tangente pode ser utilizada para calcular casas decimais do número $\pi $.

Para iniciarmos, precisamos fazer algumas apresentações a respeito de séries geométricas e séries alternadas. É recomendado ao leitor alguma habilidade sobre sequências e séries. Para um estudo mais aprofundado sobre estas e outras séries recomendamos [8, Swokowski].

Definição 4.1   Dada uma sequência geométrica infinita $\{ ar^{n} \}_{n \geq 0}$, a soma dos termos desta sequência é chamada de série geométrica. É uma expressão da forma
$\displaystyle \sum_{n=0}^{\infty} a r^{n} = a + a r + a r^{2} + a r^{3} + \dots + a r^{n} + \cdots. $

No caso de a soma infinita existir e ser igual a um número real $S$, então dizemos que a série é convergente, ou ainda, convergente para $S$. No caso em que a soma não existir então a série é dita divergente. Como casos particulares, observe que se $r = 0$ então a soma é igual a $a$ e portanto convergente e se $r = 1$ então a soma é $\infty \cdot a = \infty$ e portanto divergente.

Teorema 4.2   Uma série geométrica, $\sum ar^{n}$, é convergente, se e somente se, $\vert r\vert < 1$. No caso de convergir, o valor desta soma é precisamente o número $S = \frac{a}{1-r}$.
Definição 4.3   Se $\{ a_{n} \}_{n \geq 0}$ é uma sequência infinita de termos positivos, então uma série alternada é uma soma da forma,
$\displaystyle \sum_{n=0}^{\infty} (-1)^{n} a_{n} = a_{0} - a_{1} + a_{2} - a_{3} + \cdots + (-1)^{n} a_{n} + \cdots $
Teorema 4.4   Uma série alternada $\sum (-1)^{n}a_{n}$ é convergente se os termos $a_{n}$ formam uma sequência positiva, decrescente, e que tende a zero.

O leitor interessado nas demonstrações dos dois últimos teoremas, ou em alguns exemplos de séries alternadas e geométricas, pode consultar [8, Swokowski].

Consideremos então que $x$ seja uma variável real que assume valores no intervalo $(-1,1)$. Então $x^{2} \in [0,1)$. Podemos assim, construir uma série geométrica com primeiro termo igual a 1 e razão $r = -x^{2}$, que de acordo com o teorema 4.2, é convergente para o número $S = \frac{1}{1-r} = \frac{1}{1+x^{2}}$, já que $\vert r\vert = x^{2} < 1$. Temos então que,

$\displaystyle \frac{1}{1+x^{2}} = \sum_{n=0}^{\infty} (-1)^{n}(x^{2})^{n} = 1 - x^{2} + x^{4} - x^{6} + \cdots + (-1)^{n}x^{2n} + \cdots,$ (4.1)

para qualquer $x \in (-1,1)$. Observe que esta é uma série geométrica, mas também é uma série alternada. Podemos ainda dizer que esta série é uma série de potências de $x$, uma vez que seus termos são potências da variável $x$.

Lembremos agora que a fração $\frac{1}{1+x^{2}}$, vista como função de $x$, é a derivada da função $y = {\mathrm {tg}}^{-1}(x)$, exatamente como vimos na seção (1.7). Em outras palavras,

$\displaystyle \frac{d}{dx} ({\mathrm {tg}}^{-1} x) = \frac{1}{1+x^{2}}, $

e isto significa que,

$\displaystyle {\mathrm {tg}}^{-1} x = \int \frac{1}{1+x^{2}} dx = \int \left( \sum_{n=0}^{\infty} (-1)^{n} x^{2n} \right) dx. $

Recorremos agora ao teorema que garante a integração de uma série de potências. A demonstração deste resultado também pode ser encontrada em [8, Swokowski].

Teorema 4.5   Se uma função $f(x)$ possui representação em série de potência de $x$, isto é, $f(x) = \sum a_{n}x^{n}$ e esta série for convergente em todo $x \in (-c,c) \subset \mathbb{R}$, então
$\displaystyle \int f(x) dx = \int \left( \sum_{n=0}^{\infty} a_{n} x^{n} \right) dx = \sum_{n=0}^{\infty} \left( \int a_{n} x^{n} dx \right), $
para todo $x \in (-c,c)$. A convergência da nova série obtida pela integração dos termos, pode ser alterada se $x = \pm c$.

Este teorema nos permite então determinar, por integração, a série da função arco tangente. Temos assim,

$\displaystyle {\mathrm {tg}}^{-1} x$ $\displaystyle = \int \frac{1}{1+x^{2}} dx = \int \left( \sum_{n=0}^{\infty} (-1)^{n} x^{2n} \right) dx$    
  $\displaystyle = \sum_{n=0}^{\infty} \left( \int (-1)^{n} x^{2n} dx \right)$    
  $\displaystyle = \sum_{n=0}^{\infty} \frac{(-1)^{n} x^{2n+1}}{2n+1}$    
  $\displaystyle = x - \frac{x^{3}}{3} + \frac{x^{5}}{5} - \frac{x^{7}}{7} + \cdots + \frac{(-1)^{n} x^{2n+1}}{2n+1} + \cdots$    

e, assim, obtemos a igualdade desejada para o nosso objetivo,

$\displaystyle {\mathrm {tg}}^{-1} x = x - \frac{x^{3}}{3} + \frac{x^{5}}{5} - \... ...{9}}{9} - \frac{x^{11}}{11} + \cdots + \frac{(-1)^{n} x^{2n+1}}{2n+1} + \cdots.$ (4.2)

Esta igualdade é válida para todo $x$ no intervalo $(-1,1)$. O ponto $x = 1$, deve ser avaliado novamente pois é um dos extremos do intervalo de convergência. Para ser mais preciso, a série geométrica (4.1) é divergente no ponto $x = 1$. Mas como o teorema 4.5 afirma que a convergência pode ser alterada nos extremos do intervalo, precisamos de uma nova investigação para nos certificarmos de que a série de interesse (4.2), tornou-se convergente em $x = 1$. Note que para $x = 1$, a série em (4.2) torna-se,

$\displaystyle 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{11} + \cdots = \sum_{n=0}^{\infty} (-1)^{n} \frac{1}{2n+1} $

que é uma série alternada que satisfaz as condições do teorema 4.4 e portanto é convergente. A série (4.2) também converge se $x = -1$, mas como este valor de $x$ está fora do nosso interesse, deixaremos os detalhes para o leitor interessado.

Segue que a igualdade (4.2) é válida também para $x = 1$ e como sabemos que ${\mathrm {tg}}^{-1} 1 = \frac{\pi}{4}$, então temos a fórmula,

$\displaystyle \frac{\pi}{4} = {\mathrm {tg}}^{-1} 1 = 1 - \frac{1}{3} + \frac{1... ...c{1}{9} - \frac{1}{11} + \cdots = \sum_{n=0}^{\infty} \frac{(-1)^{n}}{2n+1}, $

ou, ainda,

$\displaystyle \pi = 4 - \frac{4}{3} + \frac{4}{5} - \frac{4}{7} + \frac{4}{9} - \frac{4}{11} + \cdots = \sum_{n=0}^{\infty} \frac{(-1)^{n}4}{2n+1}.$ (4.3)

Esta expressão, obtida por volta de 1670, é conhecida como fórmula de Gregory-Leibniz. O problema desta fórmula é que a convergência se dá de forma muito lenta, pois a série em (4.2) converge para $x$ no intervalo $[-1,1]$ e como se pode ver, o ponto $x = 1$ utilizado para obter a série está no extremo do intervalo. Quanto mais afastado do centro deste intervalo, mais lenta a convergência. Não vamos discutir aqui os chamados “níveis de convergência” e então para nós, convergência mais rápida significa obter mais casas decimais corretas com menos termos adicionados.

Vamos exemplificar o uso desta fórmula calculando uma aproximação para $\pi $ usando as 30 primeiras parcelas da soma infinita.


Tabela 4.1: Aproximação de $\pi $ pela série de Gregory-Leibniz.
$n$      $(-1)^{n}\dfrac{4}{2n+1}$      $\approx \, \pi$
         
0   4,0000000   4,0000000
1   -1,3333333   2,6666667
2   0,8000000   3,4666667
3   -0,5714286   2,8952381
4   0,4444444   3,3396825
5   -0,3636364   2,9760461
6   0,3076923   3,2837384
7   -0,2666667   3,0170717
8   0,2352941   3,2523658
9   -0,2105263   3,0418395
10   0,1904762   3,2323157
11   -0,1739130   3,0584027
12   0,1600000   3,2184027
13   -0,1481481   3,0702546
14   0,1379310   3,2081856
15   -0,1290323   3,0791533
16   0,1212121   3,2003654
17   -0,1142857   3,0860797
18   0,1081081   3,1941878
19   -0,1025641   3,0916237
20   0,0975610   3,1891847
21   -0,0930233   3,0961614
22   0,0888889   3,1850503
23   -0,0851064   3,0999439
24   0,0816327   3,1815766
25   -0,0784314   3,1031452
26   0,0754717   3,1786169
27   -0,0727273   3,1058896
28   0,0701754   3,1760650
29   -0,0677966   3,1082684
       

Note pela tabela acima, que a primeira casa decimal de $\pi $, somente estabiliza-se quando já foram somados 25 termos. Serão necessários 300 termos da série para que a segunda casa decimal seja igual a 4 e 5000 termos para obtermos a terceira casa decimal. Apesar disto, esta fórmula está longe de ser considerada inútil.

Algum tempo mais tarde, John Machin descobriu que a fórmula (4.2) poderia ser usada para valores de $x$ menores do que 1, obtendo assim, convergências mais rápidas. O problema é que não podemos simplesmente substituir $x = \frac{1}{2}$, ou $x = \frac{1}{10}$ em (4.2) pois não conhecemos ${\mathrm {tg}}^{-1}(\frac{1}{2})$ ou ${\mathrm {tg}}^{-1}(\frac{1}{10})$. É necessário um argumento mais engenhoso.

Machin usou a fórmula da soma de arcos para a tangente

$\displaystyle {\mathrm {tg}}(u+v) = \frac{{\mathrm {tg}}u + {\mathrm {tg}}v}{1- {\mathrm {tg}}u {\mathrm {tg}}v}, $

e obteve a identidade

$\displaystyle {\mathrm {tg}}\left(x - \frac{\pi}{4}\right) = \frac{{\mathrm {tg}}x -1}{1 + {\mathrm {tg}}x}, $

e com $x = 4{\mathrm {tg}}^{-1}(\frac{1}{5})$, escreveu

$\displaystyle {\mathrm {tg}}\left(4{\mathrm {tg}}^{-1}(\tfrac{1}{5}) - \frac{\p... ...^{-1}(\frac{1}{5})) -1}{1 + {\mathrm {tg}}(4{\mathrm {tg}}^{-1}(\frac{1}{5}))}.$ (4.4)

Usando a fórmula da duplicação de arcos para a tangente, Machin calculou

$\displaystyle {\mathrm {tg}}(2{\mathrm {tg}}^{-1}(\tfrac{1}{5})) = \frac{2{\mat... ...frac{1}{5}))} = \frac{2 \cdot \frac{1}{5}}{1 - \frac{1}{25}} = \frac{5}{12}, $

e depois

$\displaystyle {\mathrm {tg}}(4{\mathrm {tg}}^{-1}(\tfrac{1}{5})) = \frac{2{\mat... ...5}))} = \frac{2 \cdot \frac{5}{12}}{1-(\frac{5}{12})^{2}} = \frac{120}{119}, $

que substituído em (4.4) o levou a

$\displaystyle {\mathrm {tg}}\left(4{\mathrm {tg}}^{-1}(\tfrac{1}{5}) - \frac{\pi}{4}\right) = \frac{\frac{120}{119}-1}{1+\frac{120}{119}} = \frac{1}{239}. $

Aplicando arco tangente em ambos os membros e reorganizando os termos obtém-se a fórmula

$\displaystyle \frac{\pi}{4} = 4 {\mathrm {tg}}^{-1}(\tfrac{1}{5}) - {\mathrm {tg}}^{-1}(\tfrac{1}{239}), $

que em 1706 foi usada por Machin para calcular 100 casas decimais para $\pi $.

A ideia de Machin, de reescrever ${\mathrm {tg}}^{-1} 1$ em somas de arco tangentes com argumentos menores, motivou outros matemáticos. A igualdade

$\displaystyle {\mathrm {tg}}^{-1}( \tfrac{1}{z} ) = {\mathrm {tg}}^{-1}( \tfrac{1}{m} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{n} ),$ (4.5)

com $z$, $m$ e $n$ inteiros, se mostrou útil nesta abordagem. Note que se $z$, $m$ e $n$ são inteiros positivos, então o fato de a função arco tangente ser crescente obrigará os valores de $\frac{1}{m}$ e $\frac{1}{n}$ serem menores do que $\frac{1}{z}$. Isto significa que $\frac{1}{m}$ e $\frac{1}{n}$ estarão mais próximos de 0 do que $\frac{1}{z}$, o que torna a convergência mais rápida. Vamos primeiramente estabelecer qual a relação entre $z$, $m$ e $n$ para que a identidade (4.5) tenha sentido.

Aplicando a função tangente em ambos os membros de (4.5), temos

$\displaystyle \frac{1}{z} = {\mathrm {tg}}( {\mathrm {tg}}^{-1}( \tfrac{1}{z} ))$ $\displaystyle = {\mathrm {tg}}\left( {\mathrm {tg}}^{-1}( \tfrac{1}{m} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{n} ) \right)$    
  $\displaystyle = \frac{{\mathrm {tg}}({\mathrm {tg}}^{-1}(\frac{1}{m})) + {\math... ...c{\frac{1}{m} + \frac{1}{n}}{1 - \frac{1}{m} \frac{1}{n}} = \frac{n+m}{mn - 1},$    

e portanto, obtemos que

$\displaystyle \frac{1}{z} = \frac{n+m}{mn - 1}.$

Desta igualdade, organizando os termos e somando $z^{2}$ em ambos os membros, vem

$\displaystyle mn - nz - mz + z^{2} = 1 + z^{2}, $

ou ainda

$\displaystyle (m - z)(n - z) = 1 + z^{2}.$ (4.6)

A igualdade (4.6) estabelece portanto uma relação entre $z$, $m$ e $n$, para que a identidade (4.5) faça sentido. Como estamos interessados em desmembrar ${\mathrm {tg}}^{-1} 1$ então faremos $z = 1$ em (4.5) e (4.6), obtendo

$\displaystyle (m-1)(n-1) = 2. $

Basta então considerar $(m-1)$ e $(n-1)$ como sendo dois fatores inteiros do número 2. Escolhemos os fatores 1 e 2. Colocando $(m-1)=1$ e $(n-1) = 2$ obtemos $m = 2$ e $n = 3$ e, substituindo em (4.5), temos a fórmula

$\displaystyle \frac{\pi}{4} = {\mathrm {tg}}^{-1} 1 = {\mathrm {tg}}^{-1}( \tfrac{1}{2} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{3} ),$ (4.7)

que foi obtida por Euler em 1738.

Observe que podemos novamente repetir esta ideia para modificar as arco tangentes das frações $\frac{1}{2}$ ou $\frac{1}{3}$ por outra soma de arco tangentes com argumentos menores ainda, para fazer convergências mais rápidas.

Este foi um método muito utilizado por matemáticos e várias fórmulas foram obtidas, conhecidas como fórmulas do tipo Machin. Algumas delas são:

$\displaystyle \frac{\pi}{4}$ $\displaystyle = {\mathrm {tg}}^{-1}( \tfrac{1}{2} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{5} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{8} )$ (Strassnitzky)
$\displaystyle \frac{\pi}{4}$ $\displaystyle = 2 {\mathrm {tg}}^{-1}( \tfrac{1}{3} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{7} )$ (Huton)
$\displaystyle \frac{\pi}{4}$ $\displaystyle = 4 {\mathrm {tg}}^{-1}(\tfrac{1}{5}) - {\mathrm {tg}}^{-1}(\tfrac{1}{70}) + {\mathrm {tg}}^{-1}(\tfrac{1}{99})$ (Euler, em 1764)
$\displaystyle \frac{\pi}{4}$ $\displaystyle = 8 {\mathrm {tg}}^{-1}( \tfrac{1}{10} ) - {\mathrm {tg}}^{-1}( \tfrac{1}{239} ) - 4 {\mathrm {tg}}^{-1}( \tfrac{1}{515} )$ (Klingenstierna)
$\displaystyle \frac{\pi}{4}$ $\displaystyle = 12 {\mathrm {tg}}^{-1}(\tfrac{1}{18}) + 8 {\mathrm {tg}}^{-1}(\tfrac{1}{57}) - 5 {\mathrm {tg}}^{-1}( \tfrac{1}{239} )$ (Gauss)
$\displaystyle \frac{\pi}{4}$ $\displaystyle = 3 {\mathrm {tg}}^{-1}(\tfrac{1}{4}) + {\mathrm {tg}}^{-1}(\tfrac{1}{20}) + {\mathrm {tg}}^{-1}(\tfrac{1}{1985})$ (Loney, em 1893)
$\displaystyle \frac{\pi}{4}$ $\displaystyle = 22 {\mathrm {tg}}^{-1}(\tfrac{1}{38}) + 17 {\mathrm {tg}}^{-1}(\tfrac{7}{601}) + 10 {\mathrm {tg}}^{-1}(\tfrac{7}{8149})$ (Sebah)
$\displaystyle \frac{\pi}{4}$ $\displaystyle = 44 {\mathrm {tg}}^{-1}(\tfrac{1}{57}) + 7 {\mathrm {tg}}^{-1}(\... ... {\mathrm {tg}}^{-1}(\tfrac{1}{682}) + 24 {\mathrm {tg}}^{-1}(\tfrac{1}{12943})$ (Stormer, em 1896)
$\displaystyle \frac{\pi}{4}$ $\displaystyle = 12 {\mathrm {tg}}^{-1}(\tfrac{1}{49}) + 32 {\mathrm {tg}}^{-1}(... ...{\mathrm {tg}}^{-1}(\tfrac{1}{239}) + 12 {\mathrm {tg}}^{-1}(\tfrac{1}{110443})$ (Takano, em 1982)

A fórmula de Strassnitzky, é obtida a partir da fórmula de Euler, desmembrando o termo ${\mathrm {tg}}^{-1}( \frac{1}{3} )$. Vamos ver os detalhes. Considerando $\frac{1}{z} = \frac{1}{3}$ e, portanto, $z = 3$, em (4.5) e (4.6), obtemos

$\displaystyle (m-3)(n-3) = 10. $

Escolhemos agora dois fatores de 10. Considerando os fatores 2 e 5 e colocando $(m-3)=2$ e $(n-3)=5$, obtemos $m = 5$ e $n = 8$. Temos portanto

$\displaystyle \frac{\pi}{4}$ $\displaystyle = {\mathrm {tg}}^{-1}( \tfrac{1}{2} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{3} )$    
  $\displaystyle = {\mathrm {tg}}^{-1}( \tfrac{1}{2} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{5} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{8} ).$    

A fórmula de Huton é obtida, também a partir da fórmula de Euler, desmembrando o termo ${\mathrm {tg}}^{-1}(\frac{1}{2})$. Considerando $\frac{1}{z} = \frac{1}{2}$, isto é, $z=2$ e, substituindo em (4.5) e (4.6), temos

$\displaystyle (m-2)(n-2) = 5, $

e escolhendo $(m-2) = 1$ e $(n-2) = 5$ temos $m = 3$ e $n = 7$ e com estes valores

$\displaystyle \frac{\pi}{4}$ $\displaystyle = {\mathrm {tg}}^{-1}( \tfrac{1}{2} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{3} )$    
  $\displaystyle = {\mathrm {tg}}^{-1}( \tfrac{1}{3} ) + {\mathrm {tg}}^{-1}( \tfr... ... = 2 {\mathrm {tg}}^{-1}( \tfrac{1}{3} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{7} ).$    

Levando em conta ainda que podemos considerar que os fatores, $m$ e $n$, do número $z^{2}+1$ sejam inteiros negativos, e usando o fato de que arco tangente é uma função ímpar, isto é, ${\mathrm {tg}}^{-1}(-\frac{1}{n}) = - {\mathrm {tg}}^{-1}(\frac{1}{n})$, conseguimos o cancelamento de termos em algumas substituições. Mais ainda, $z$, $m$ e $n$ não precisam ser números inteiros, já que o desenvolvimento aplicado em (4.5) é válido para quaisquer argumentos reais no domínio da função arco tangente.

Podemos verificar que

$\displaystyle {\mathrm {tg}}^{-1}(\tfrac{1}{3}) = {\mathrm {tg}}^{-1}(\tfrac{1}{7}) + {\mathrm {tg}}^{-1}(\tfrac{2}{11}), $

e que

$\displaystyle {\mathrm {tg}}^{-1}(\tfrac{2}{11}) = {\mathrm {tg}}^{-1}(\tfrac{1}{7}) + {\mathrm {tg}}^{-1}(\tfrac{3}{79}), $

e substituindo estas duas igualdades na fórmula de Huton, obtém-se

$\displaystyle \frac{\pi}{4}$ $\displaystyle = 2 {\mathrm {tg}}^{-1}( \tfrac{1}{3} ) + {\mathrm {tg}}^{-1}( \tfrac{1}{7} )$    
  $\displaystyle = 3 {\mathrm {tg}}^{-1}(\tfrac{1}{7}) + 2{\mathrm {tg}}^{-1}(\tfrac{2}{11})$    
  $\displaystyle = 5 {\mathrm {tg}}^{-1}(\tfrac{1}{7}) + {\mathrm {tg}}^{-1}(\tfrac{3}{79}).$    

Vamos comparar os resultados obtidos na tabela 4.1, calculando agora uma aproximação de $\pi $ pela série de Euler (4.7). Fazendo $x = \frac{1}{2}$ e $x = \frac{1}{3}$ em (4.2), temos

$\displaystyle {\mathrm {tg}}^{-1}(\tfrac{1}{2}) = \sum_{n=0}^{\infty} \frac{(-1)^{n}}{2^{2n+1}(2n+1)},$   e$\displaystyle \qquad {\mathrm {tg}}^{-1}(\tfrac{1}{3}) = \sum_{n=0}^{\infty} \frac{(-1)^{n}}{3^{2n+1}(2n+1)}. $

Então temos que,

$\displaystyle \pi = 4{\mathrm {tg}}^{-1}(\tfrac{1}{2}) + 4{\mathrm {tg}}^{-1}(\... ...ac{4}{2^{2n+1}(2n+1)} + \sum_{n=0}^{\infty} (-1)^{n} \frac{4}{3^{2n+1}(2n+1)}. $

Abaixo segue uma tabela de convergência para $\pi $ com os 15 primeiros termos desta última série.


Tabela 4.2: Aproximação de $\pi $ pela série de Euler.
$n$ $S_{1} = \frac{(-1)^{n}4}{2^{2n+1}(2n+1)}$ $S_{2} = \frac{(-1)^{n}4}{3^{2n+1}(2n+1)}$ $S_{1} + S_{2}$      $\approx \pi$
         
0 2,0000000000 1,3333333333 3,3333333333 3,3333333333
1 -0,1666666667 -0,0493827160 -0,2160493827 3,1172839506
2 0,0250000000 0,0032921811 0,0282921811 3,1455761317
3 -0,0044642857 -0,0002612842 -0,0047255699 3,1408505618
4 0,0008680556 0,0000225801 0,0008906357 3,1417411974
5 -0,0001775568 -0,0000020527 -0,0001796096 3,1415615879
6 0,0000375601 0,0000001930 0,0000377531 3,1415993410
7 -0,0000081380 -0,0000000186 -0,0000081566 3,1415911844
8 0,0000017952 0,0000000018 0,0000017970 3,1415929813
9 -0,0000004015 -0,0000000002 -0,0000004017 3,1415925796
10 0,0000000908 0,0000000000 0,0000000908 3,1415926705
11 -0,0000000207 -0,0000000000 -0,0000000207 3,1415926497
12 0,0000000048 0,0000000000 0,0000000048 3,1415926545
13 -0,0000000011 -0,0000000000 -0,0000000011 3,1415926534
14 0,0000000003 0,0000000000 0,0000000003 3,1415926536
         

Observe que esta série converge muito mais rápido do que a série (4.3). Com apenas 15 termos somados, temos 9 casas decimais corretas de $\pi $. Note ainda que na terceira coluna, os valores vão para zero mais rápido do que na segunda coluna. Como dissemos antes, isto ocorre pois a terceira coluna representa os valores da série arco tangente de $\frac{1}{3}$ e $\frac{1}{3}$ está mais próximo de 0 do que $\frac{1}{2}$.

Atualmente o trabalho de calcular $\pi $ é feito com o auxílio de supercomputadores, que trabalham por horas ou até dias para calcular trilhões de casas decimais. As fórmulas baseadas em arco tangente são bastante utilizadas por apresentarem apenas números racionais.

A questão principal é por que calcular $\pi $ com trilhões de casas decimais? Sabe-se que umas poucas casas decimais resolvem todos os problemas práticos de engenharia, física ou matemática. Para ser mais preciso, 39 casas decimais permitem calcular a medida da circunferência do universo com erro menor do que o diâmetro de um átomo de hidrogênio.

Uma aplicação prática é o teste de microprocessadores. Quando um computador ou um processador numérico é desenvolvido, é necessário saber até que ponto sua eficiência numérica é confiável, e nestes termos, nada melhor do que testá-lo a calcular um número já conhecido. Calcular dígitos de $\pi $, já não é mais uma questão de conhecer este número, mas sim de comprovar o poder dos computadores.

Para uma coleção maior de fórmulas envolvendo $\pi $ recomendamos [6, Sebah], [1, Eymard] e também [9, Weisstein]. Comentários e demonstrações sobre outras fórmulas para $\pi $ podem ser encontrados em [1, Eymard].

4.2 Cálculo de integrais

Dentre as aplicações clássicas e imediatas do Cálculo Diferencial e Integral estão o cálculo de áreas de regiões e de comprimentos de curvas determinadas por funções. Estes cálculos em geral reduzem-se ao cálculo de integrais envolvendo tais funções. Entretanto, determinar certas integrais não é tarefa tão fácil. Existem várias regras de integração porém muitas funções não se enquadram nas técnicas tradicionais de integração.

Dentre várias situações podemos citar como exemplo

$\displaystyle \int \sqrt{r^{2}-x^{2}}dx$   e$\displaystyle \qquad \int \sqrt{r^{2}+x^{2}} dx,$ (4.8)

para $r>0$ uma constante e $x$ no devido intervalo de definição das funções consideradas.

A primeira integral aparece, por exemplo, no cálculo de áreas de regiões circulares. Mais precisamente, dado $r>0$, a área $A$ compreendida entre o eixo $x$ e o gráfico do semi-círculo $f(x) = \sqrt{r^{2}-x^{2}}$, no intervalo $[a,b] \subset [-r,r]$, é calculada pela integral definida

$\displaystyle A = \int_{a}^{b} \sqrt{r^{2}-x^{2}} dx. $
Figura 4.1: Área sob a semicircunferência.
Image areaint

A segunda integral em (4.8) aparece, por exemplo, no cálculo de comprimento de curvas. O comprimento $C$ da curva determinada pelo gráfico de uma função quadrática $g(x) = kx^{2}$, para alguma constante $k \in \mathbb{R}$, no intervalo $[a,b] \subset \mathbb{R}$, é dado por

$\displaystyle C = \int_{a}^{b} \sqrt{1+[g'(x)]^{2}} dx = \frac{1}{r} \int_{a}^{b} \sqrt{r^{2}+x^{2}} dx, $

sendo que $r = \frac{1}{2k}$ tornou-se uma constante de ajuste.

O aluno de um curso de Cálculo Diferencial e Integral, quando se depara com alguma das integrais em (4.8), recorre às fórmulas de integração prontas que geralmente figuram nas últimas páginas dos livros. Mas estas fórmulas não “caíram do céu”. Nesta seção vamos mostrar como as funções trigonométricas podem ajudar a determinar as integrais em (4.8). Não vamos nos preocupar com o intervalo $[a,b]$ e então faremos os cálculos considerando as integrais indefinidas.

Para a primeira integral em (4.8), precisaremos antes o cálculo auxiliar da integral

$\displaystyle \int \cos^{2}x dx. $

Usando as identidades

  $\displaystyle \cos^{2}x + {\mathrm {sen}}^{2}x = 1,$    
  $\displaystyle \cos^{2}x - {\mathrm {sen}}^{2}x = \cos(2x),$    

obtemos

$\displaystyle \cos^{2}x = \tfrac{1}{2} + \tfrac{1}{2} \cos(2x), $

e, também,

$\displaystyle {\mathrm {sen}}^{2}x = \tfrac{1}{2} - \tfrac{1}{2} \cos(2x). $

Integrando temos

$\displaystyle \int \cos^{2}x dx$ $\displaystyle = \tfrac{1}{2}x + \tfrac{1}{4} {\mathrm {sen}}(2x),$    
$\displaystyle \int {\mathrm {sen}}^{2}x dx$ $\displaystyle = \tfrac{1}{2}x - \tfrac{1}{4} {\mathrm {sen}}(2x).$    

O leitor atento diria agora que esquecemos a constante de integração nas duas expressões acima. Por simplicidade, durante os cálculos omitiremos a constante de integração, que só será apresentada ao final para não perder definitivamente o rigor matemático. Agora vamos ao cálculo da primeira integral em (4.8). Considerando que $x \in [-r,r]$, queremos determinar

$\displaystyle \int \sqrt{r^{2}-x^{2}}dx. $

Fazendo a mudança de variáveis $x = r{\mathrm {sen}}t$, temos que $\frac{dx}{dt} = r \cos t$ e, substituindo na integral, temos

$\displaystyle \int \sqrt{r^{2}-x^{2}}dx$ $\displaystyle = \int \sqrt{r^{2}-(r{\mathrm {sen}}t)^{2}} \,\, r \cos t dt$    
  $\displaystyle = \int r\sqrt{1- {\mathrm {sen}}^{2} t} \,\, r \cos t dt = r^{2} \int \sqrt{\cos^{2} t} \cos t dt.$    

Lembremos agora que $x \in [-r,r]$ e então a substituição $x = r{\mathrm {sen}}t$ obriga (bijetivamente) $t \in [-\frac{\pi}{2}, \frac{\pi}{2}]$. Neste intervalo temos $\cos t > 0$ e então

$\displaystyle \int \sqrt{r^{2}-x^{2}}dx$ $\displaystyle = r^{2} \int \sqrt{\cos^{2} t} \cos t dt = r^{2} \int \cos t \cos t dt$    
  $\displaystyle = r^{2} \int \cos^{2} t dt = r^{2} (\tfrac{1}{2}t + \tfrac{1}{4} {\mathrm {sen}}(2t)) = \frac{r^{2}}{2}t + \frac{r^{2}}{2} {\mathrm {sen}}t \cos t.$    

Voltando à variável original $x$, temos que ${\mathrm {sen}}t = \frac{x}{r}$, ou ainda $t = {\mathrm {sen}}^{-1}(\frac{x}{r})$ e, assim,

$\displaystyle \int \sqrt{r^{2}-x^{2}}dx$ $\displaystyle = \frac{r^{2}}{2}t + \frac{r^{2}}{2} {\mathrm {sen}}t \cos t$    
  $\displaystyle = \frac{r^{2}}{2} {\mathrm {sen}}^{-1}(\tfrac{x}{r}) + \frac{r^{2... ...^{2}}{2} {\mathrm {sen}}^{-1}(\tfrac{x}{r}) + \frac{1}{2} x \sqrt{r^{2}-x^{2}}.$    

Obtemos então a fórmula de integração presente nos livros de Cálculo Diferencial e Integral

$\displaystyle \int \sqrt{r^{2}-x^{2}}dx = \frac{r^{2}}{2} {\mathrm {sen}}^{-1}(\tfrac{x}{r}) + \frac{x}{2} \sqrt{r^{2}-x^{2}} + C, $

para alguma constante de integração $C$.

A segunda integral em (4.8) é obtida de forma análoga porém com funções trigonométricas hiperbólicas. Primeiro vamos determinar a integral

$\displaystyle \int \cosh^{2}x dx. $

Usando as identidades

  $\displaystyle \cosh^{2}x - {\mathrm{senh}}^{2}x = 1,$    
  $\displaystyle \cosh^{2}x + {\mathrm{senh}}^{2}x = \cosh(2x),$    

temos que

$\displaystyle \cosh^{2}x = \tfrac{1}{2} + \tfrac{1}{2} \cosh(2x),$    
$\displaystyle {\mathrm{senh}}^{2}x = \tfrac{1}{2} \cosh(2x) - \tfrac{1}{2},$    

e integrando

$\displaystyle \int \cosh^{2}x dx = \tfrac{1}{4} {\mathrm{senh}}(2x) + \tfrac{1}{2}x,$    
$\displaystyle \int {\mathrm{senh}}^{2}x dx = \tfrac{1}{4} {\mathrm{senh}}(2x) - \tfrac{1}{2}x.$    

Vamos agora determinar a integral de interesse,

$\displaystyle \int \sqrt{r^{2}+x^{2}} dx, $

considerando $x \in \mathbb{R}$ e $r>0$ uma constante arbitrária. Fazendo a mudança de variáveis $x = r {\mathrm{senh}}t$ temos que $\frac{dx}{dt} = r \cosh t$ e então temos

$\displaystyle \int \sqrt{r^{2}+x^{2}} dx$ $\displaystyle = \int \sqrt{r^{2}+(r {\mathrm{senh}}t)^{2}} \,\, r \cosh t dt$    
  $\displaystyle = \int r \sqrt{1+{\mathrm{senh}}^{2} t} \,\, r \cosh t dt$    
  $\displaystyle = r^{2} \int \sqrt{1+{\mathrm{senh}}^{2} t} \,\, \cosh t dt = r^{2} \int \sqrt{\cosh^{2} t} \,\, \cosh t dt.$    

Lembrando agora que a função seno hiperbólico é bijetiva de $\mathbb{R}$ em $\mathbb{R}$ e então a mudança de variável $x = r {\mathrm{senh}}t$ permite $t \in \mathbb{R}$ e como $\cosh t > 0$ para qualquer $t \in \mathbb{R}$, temos

$\displaystyle \int \sqrt{r^{2}+x^{2}} dx$ $\displaystyle = r^{2} \int \sqrt{\cosh^{2} t} \,\, \cosh t dt$    
  $\displaystyle = r^{2} \int \cosh t \,\, \cosh t dt$    
  $\displaystyle = r^{2}( \tfrac{1}{4} {\mathrm{senh}}(2t) + \tfrac{1}{2}t) = \frac{r^{2}}{2} {\mathrm{senh}}t \cosh t + \frac{r^{2}}{2}t,$    

e voltando à variável $x$, temos ${\mathrm{senh}}t = \frac{x}{r}$, ou ainda $t = {\mathrm{senh}}^{-1}(\frac{x}{r})$ e, assim,

$\displaystyle \int \sqrt{r^{2}+x^{2}} dx$ $\displaystyle = \frac{r^{2}}{2} {\mathrm{senh}}t \cosh t + \frac{r^{2}}{2}t$    
  $\displaystyle = \frac{r^{2}}{2} \frac{x}{r} \sqrt{1+\frac{x^{2}}{r^{2}}} + \fra... ...{x}{2} \sqrt{r^{2}+x^{2}} + \frac{r^{2}}{2} {\mathrm{senh}}^{-1}(\tfrac{x}{r}).$    

Neste caso, podemos escrever esta igualdade sem o uso explícito da função arco seno hiperbólico. Usando a identidade ${\mathrm{senh}}^{-1} x = \ln(x + \sqrt{x^{2} + 1})$, obtida na seção 3.3, escrevemos

$\displaystyle \int \sqrt{r^{2}+x^{2}} dx = \frac{x}{2} \sqrt{r^{2}+x^{2}} + \frac{r^{2}}{2} \ln\left( \tfrac{x}{r} + \sqrt{\tfrac{x^{2}}{r^{2}} + 1} \right), $

e, reorganizando os termos temos, finalmente

$\displaystyle \int \sqrt{r^{2}+x^{2}} dx = \frac{x}{2} \sqrt{r^{2}+x^{2}} + \frac{r^{2}}{2} \ln\left( x + \sqrt{x^{2} + r^{2}} \right) + C, $

sendo que a constante de integração $C$ absorve o termo constante $-\frac{r^{2}}{2} \ln r$ que desprezamos na reorganização dos termos.

A fórmula de integração

$\displaystyle \int \sqrt{x^{2}-r^{2}} dx = \frac{x}{2} \sqrt{x^{2}-r^{2}} - \frac{r^{2}}{2} \ln\left( x + \sqrt{x^{2} - r^{2}} \right) + C, $

válida para $x \geq r > 0$, é obtida de maneira análoga pela substituição $x = r \cosh t$. Deixamos agora os detalhes para o leitor.

Podemos ainda observar que em algumas situações, o cálculo da integral $\int \sqrt{r^{2}-x^{2}}dx$ não é efetuado em coordenadas cartesianas. Como é sabido, as coordenadas cartesianas dificultam o cálculo de integrais em regiões circulares. Neste tipo de região é recomendado o uso de coordenadas polares. Mas a conversão de coordenadas cartesianas para polares (e vice-versa) faz uso das funções trigonométricas também.

4.3 A catenária

Catenária é o nome da curva que descreve a trajetória de equilíbrio de um cabo flexível, de comprimento fixo e suspenso por duas hastes. O estudo desta curva desempenha um papel fundamental nos cursos de engenharia.

Consideremos então um cabo flexível, sustentado por duas hastes, pelos pontos $A$ e $B$. Fixemos um sistema coordenado cartesiano com o eixo $Ox$ no nível do solo e o eixo $Oy$ perpendicular ao solo passando pelo ponto mais baixo do cabo. O cabo descreve uma curva neste sistema coordenado. Denotemos por $y = f(x)$ esta curva. Chamemos $C = (0,c)$ o ponto mais baixo da curva, que está sobre o eixo $Oy$. Tomemos um ponto $P = (x,y)$ sobre esta curva e sem perda de generalidade, consideremos o ponto $P$ à direita de $C$ no sistema coordenado considerado, isto é, $P = (x,y)$ com $x>0$.

Considerando a porção do cabo entre os pontos $C$ e $P$, temos as forças $\vec{h}$, $\vec{p}$ e $\vec{t}$, atuando sobre esta porção do cabo. $\vec{p}$ é a força peso, que é decomposta nas componentes horizontal e vertical por

$\displaystyle \vec{p} = (0, -\omega L) $

sendo que $\omega$ é o peso do cabo por unidade de comprimento e $L$ é o comprimento do cabo (da porção do cabo considerada). $\vec{t}$ é a força de tração pela direita no ponto $P = (x,y)$ e é decomposta nas componentes horizontal e vertical por

$\displaystyle \vec{t} = (t \cos \theta, t {\mathrm {sen}}\theta), $

sendo $t$ o módulo da tensão pela direita e $\theta$ o ângulo que o vetor tangencial $\vec{t}$ faz com a horizontal. $\vec{h}$ é a força de tração pela esquerda no ponto $C = (0,c)$, dada por

$\displaystyle \vec{h} = (-h,0), $

sendo $h$ o módulo da tensão pela esquerda.

Figura 4.2: Forças atuantes no cabo suspenso.
Image catenaria

O sistema está em equilíbrio, isto é,

$\displaystyle \vec{h} + \vec{p} + \vec{t} = \vec{0}, $

e então

$\displaystyle (-h,0) + (0,-\omega L) + (t \cos \theta, t {\mathrm {sen}}\theta) = (0,0), $

donde temos

  $\displaystyle -h + t \cos \theta = 0$    
  $\displaystyle -\omega L + t {\mathrm {sen}}\theta = 0.$    

Agora, sabemos do cálculo diferencial e integral que a inclinação $\theta$, do vetor tangente à curva em um ponto $x$, se relaciona com a curva por

$\displaystyle {\mathrm {tg}}\theta = y', $

donde temos que

$\displaystyle y' = {\mathrm {tg}}\theta = \frac{{\mathrm {sen}}\theta}{\cos \theta} = \frac{\frac{\omega L}{t}}{\frac{h}{t}} = \frac{\omega L}{h}. $

Mas note que $L$ não é uma constante. $L = L(x)$ é o comprimento da curva de $C$ a $P$ e isto dependerá da posição do ponto $P = (x,y)$. Sabemos (do cálculo) que o comprimento desta curva pode ser calculado pela fórmula integral,

$\displaystyle L = L(x) = \int_{0}^{x} \sqrt{1+(y')^{2}} \,\, dx, $

e, assim,

$\displaystyle y' = \frac{\omega L}{h} = \frac{\omega}{h} \int_{0}^{x} \sqrt{1+(y')^{2}} \,\, dx. $

Para eliminar a integral do segundo membro, derivamos ambos os membros da igualdade e, usando o Teorema Fundamental do Cálculo, obtemos

$\displaystyle y'' = \frac{\omega}{h} \sqrt{1+(y')^{2}}.$ (4.9)

A esta equação diferencial, juntamos as condições iniciais $y'(0) = 0$ e $y(0) = c$. Com o intuito de encontrar $y = f(x)$, a função que descreve a curva catenária, vamos resolver esta equação diferencial. Fazendo $z=y'$ e substituindo em (4.9), temos a equação diferencial de ordem 1,

$\displaystyle z' = \tfrac{\omega}{h} \sqrt{1+z^{2}}, $

que pode ser reescrita na forma

$\displaystyle \frac{z'}{\sqrt{1+z^{2}}} = \frac{\omega}{h}. $

Integrando em $x$, obtemos

$\displaystyle \int \frac{z'}{\sqrt{1+z^{2}}} dx = \frac{\omega}{h} x + k,$ (4.10)

para alguma constante de integração $k$ que ainda será determinada. Para determinar a integral do primeiro membro, notemos que

$\displaystyle \int \frac{z'}{\sqrt{1+z^{2}}} dx = \int \frac{\frac{dz}{dx}}{\sqrt{1+z^{2}}}dx = \int \frac{1}{\sqrt{1+z^{2}}} dz. $

e levando em conta que a fração $\frac{1}{\sqrt{1+z^{2}}}$ é a derivada da função ${\mathrm{senh}}^{-1} z$ (em relação a $z$), segue que

$\displaystyle {\mathrm{senh}}^{-1} z = \int \frac{1}{\sqrt{1+z^{2}}} dz = \frac{\omega}{h}x + k, $

para alguma constante $k$.

Substituindo a condição inicial $z(0) = y'(0) = 0$, obtemos o valor da constante $k = 0$. Voltando para a variável $y$, e com $k = 0$, obtemos

$\displaystyle {\mathrm{senh}}^{-1}(y') = \frac{\omega}{h} x. $

Aplicando a função seno hiperbólico em ambos os membros, temos

$\displaystyle y' = {\mathrm{senh}}(\tfrac{\omega}{h}x), $

e integrando ambos os membros em relação a $x$, vem

$\displaystyle y = \frac{h}{\omega} \cosh(\tfrac{\omega}{h} x) + k. $

Usando a condição inicial $y(0) = c$, conseguimos o valor da nova constante de integração $k = (c-\frac{h}{\omega})$. Segue portanto a função procurada

$\displaystyle y = \frac{h}{\omega} \cosh(\tfrac{\omega}{h} x) + \left( c-\tfrac{h}{\omega} \right). $

Desta forma, obtemos que a curva catenária é descrita por um cosseno hiperbólico. O termo de translação $(c-\frac{h}{\omega})$ pode ser manipulado mudando-se a origem do sistema coordenado fixado sobre a curva catenária. Os fatores $\frac{h}{\omega}$ e $\frac{\omega}{h}$ determinam a abertura da curva.

4.4 Série de Fourier

O objetivo desta seção é apresentar as séries de Fourier. Jean Baptiste Fourier (1768-1830) foi o primeiro matemático a investigar séries envolvendo senos e cossenos e, por isso, essas séries levam hoje o seu nome. Ele introduziu esse assunto em 1822 em seu livro Théorie Analytique de la Chaleur (Teoria analítica do calor).

Consideremos uma barra de comprimento $L$, com extremos em contato com um material de temperatura constante igual a zero. Se $u(x,t)$ é a temperatura desta barra no ponto $x$ e no instante $t$, $f$ é a distribuição inicial da temperatura da barra e o fluxo de calor na extremidade da barra é proporcional à temperatura da extremidade, então a função $u(x,t)$ satisfaz as equações

$\displaystyle \left\{ \begin{array}{l} u_{t} = \alpha^{2} u_{xx} \quad \text{em... ..., \\ u(x,0) = f(x) \quad \text{para} \quad x \in [0,L], \end{array} \right. $

sendo que $u_{t} = \frac{\partial u}{\partial t}$, $u_{x} = \frac{\partial u}{\partial x}$ e $u_{xx} = \frac{\partial^{2} u}{\partial x^{2}}$.

Esta é uma equação diferencial parcial, sujeita às condições de contorno e condições iniciais. Vamos resolver esta equação. O método que usaremos é conhecido como método das variáveis separáveis.

Este método consiste em supor que a função $u(x,t)$ possa ser expressa como um produto de duas funções, uma dependendo de $t$ e outra dependendo de $x$, isto é, supomos que $u(x,t) = \varphi(x) \eta(t)$. Substituindo na equação diferencial parcial, temos

$\displaystyle \varphi(x) \eta'(t) = \alpha^{2} \eta(t) \varphi''(x), $

ou, ainda,

$\displaystyle \frac{1}{\alpha^{2}} \frac{\eta'(t)}{\eta(t)} = \frac{\varphi''(x)}{\varphi(x)}. $

Observe que o membro da direita não depende de $t$, enquanto o membro da esquerda não depende de $x$. Isto sugere que na verdade ambos os membros não dependam nem de $x$ e nem de $t$, isto é, são constantes. Fisicamente esta constante é negativa considerando que a taxa de variação da temperatura está diminuindo. Por uma questão de facilidade no desenvolvimento dos cálculos, esta constante negativa é escrita como $-\lambda$, com $\lambda > 0$.

Temos então

$\displaystyle \frac{1}{\alpha^{2}} \frac{\eta'(t)}{\eta(t)} = -\lambda$   e$\displaystyle \qquad \frac{\varphi''(x)}{\varphi(x)} = -\lambda, $

ou ainda,

$\displaystyle \eta'(t) + \lambda\alpha^{2} \eta(t) = 0$   e$\displaystyle \qquad \varphi''(x) + \lambda \varphi(x) = 0. $

Temos agora duas equações diferenciais ordinárias, lineares e homogêneas. As soluções são fáceis de serem obtidas e são, precisamente,

$\displaystyle \varphi(x)$ $\displaystyle = a\cos(\sqrt{\lambda}x) + b{\mathrm {sen}}(\sqrt{\lambda}x)$    
$\displaystyle \eta(t)$ $\displaystyle = ce^{-\lambda \alpha^{2} t}$    

para quaisquer coeficientes $a,b,c \in \mathbb{R}$. Segue que

$\displaystyle u(x,t) = \left( a\cos(\sqrt{\lambda}x) + b{\mathrm {sen}}(\sqrt{\lambda}x) \right) ce^{-\lambda \alpha^{2} t}. $

Os coeficientes $a$, $b$ e $c$ poderão ser determinados ou estimados utilizando as condições iniciais e as condições de contorno. Aplicando as condições de contorno, e já descartando a função exponencial que nunca se anula, temos que

$\displaystyle \left\{ \begin{array}{l} ca + cb\sqrt{\lambda} = 0, \\ ca\cos(... ...\lambda}L) + cb\sqrt{\lambda}\cos(\sqrt{\lambda}L) = 0. \end{array} \right. $

Vamos considerar que $c \neq 0$ pois estamos interessados em uma solução não identicamente nula. Da primeira equação obtemos que $a = -b\sqrt{\lambda}$ e, substituindo isso na segunda equação, temos

$\displaystyle b(1+\lambda) {\mathrm {sen}}(\sqrt{\lambda}L) = 0. $

Mas como $\lambda > 0$ então $(1+\lambda) \neq 0$ e, por isso, também vamos impor que $b \neq 0$, pois caso contrário, isto é, se $b = 0$ teríamos também $a = 0$ e a função $\varphi(x)$ se tornaria identicamente nula, fazendo a solução $u(x,t)$ identicamente nula. Como estamos interessados em soluções não nulas, vamos impor $b \neq 0$. Desta forma, resta que

$\displaystyle {\mathrm {sen}}(\sqrt{\lambda}L) = 0, $

donde

$\displaystyle \sqrt{\lambda} = \frac{k\pi}{L}, $

para qualquer $k \in \mathbb{Z}$. Já que o sinal do argumento no seno se transmite para o coeficiente $b$, podemos considerar que $k \in \mathbb{N}$. Sendo assim, para cada $k \in \mathbb{N}$, temos uma solução

$\displaystyle u_{k}(x,t) = \left( a_{k}\cos(\frac{k\pi}{L}x) +b_{k}{\mathrm {sen}}(\frac{k\pi}{L}x) \right) e^{-\lambda \alpha^{2} t}, $

para certos coeficientes $a_{k}$ e $b_{k}$, que já incorporaram também a constante $c$.

Pelo princípio da superposição de soluções para equações homogêneas, temos que a soma destas soluções é ainda uma solução. Segue que

$\displaystyle u(x,t) = \sum_{k=0}^{\infty} u_{k}(x,t) = \sum_{k=0}^{\infty} \le... ...L}x) +b_{k}{\mathrm {sen}}(\frac{k\pi}{L}x) \right) e^{-\lambda \alpha^{2} t}. $

Tudo o que precisamos agora é determinar os coeficientes $a_{k}$ e $b_{k}$. Aplicando a condição inicial, temos que

$\displaystyle f(x) = u(x,0) = \sum_{k=0}^{\infty} a_{k}\cos(\frac{k\pi}{L}x) + b_{k}{\mathrm {sen}}(\frac{k\pi}{L}x).$ (4.11)

Os coeficientes $a_{k}$ e $b_{k}$ procurados, são então coeficientes que satisfazem a identidade (4.11). Perguntamos então quais as hipóteses sobre $f$ para que a igualdade (4.11) se verifique para certos coeficientes $a_{k}$ e $b_{k}$ reais? Esta questão é respondida pelo teorema 4.7 enunciado mais adiante. Além disso, se a igualdade (4.11) se verificar, como são calculados os coeficientes $a_{k}$ e $b_{k}$? Esta questão será comentada agora.

Para mostrar como são calculados estes coeficientes, precisamos estudar algumas propriedades a respeito do conjunto de funções

$\displaystyle \mathcal{F} = \left\{ \cos(\frac{m\pi}{L}x); \quad m \in \mathbb{... ...\cup \left\{ {\mathrm {sen}}(\frac{n\pi}{L}x); \quad n \in \mathbb{N}\right\}. $

Consideremos o conjunto $\mathcal{C} = C([-L,L]; \mathbb{R})$, das funções contínuas e definidas no intervalo $[-L,L]$ com valores em $\mathbb{R}$. Este conjunto munido da soma de funções

$\displaystyle (f+g)(x) = f(x) + g(x) $

e do produto por escalar $a \in \mathbb{R}$,

$\displaystyle (af)(x) = a f(x), $

é um espaço vetorial real. O funcional bilinear $\langle \cdot, \cdot \rangle: \mathcal{C} \times \mathcal{C} \to \mathbb{R}$ dado por

$\displaystyle \langle f, g \rangle = \int_{-L}^{L} f(x) g(x) dx $

define um produto interno em $\mathcal{C}$. A respeito deste produto interno vemos que o conjunto $\mathcal{F}$ é um conjunto de vetores ortogonais no espaço vetorial $\mathcal{C} = C([-L,L]; \mathbb{R})$. Provaremos isto em forma de teorema.

Teorema 4.6   O conjunto de funções
$\displaystyle \mathcal{F} = \left\{ \cos(\frac{m\pi}{L}x); \quad m \in \mathbb{... ...\cup \left\{ {\mathrm {sen}}(\frac{n\pi}{L}x); \quad n \in \mathbb{N}\right\}. $

é um conjunto de funções duas a duas ortogonais do espaço vetorial $\mathcal{C} = C([-L,L]; \mathbb{R})$.

Prova. Para quaisquer $m,n \in \mathbb{N}$, temos que
$\displaystyle \int_{-L}^{L} \cos(\frac{m\pi}{L}x) {\mathrm {sen}}(\frac{n\pi}{L}x) dx = 0 $

já que o integrando é uma função ímpar.

Se $m \neq n$ então

$\displaystyle \int_{-L}^{L}$ $\displaystyle \cos(\frac{m\pi}{L}x) \cos(\frac{n\pi}{L}x) dx$    
  $\displaystyle = \frac{1}{2} \int_{-L}^{L} \cos(\frac{m\pi}{L}x+\frac{n\pi}{L}x) + \cos(\frac{m\pi}{L}x-\frac{n\pi}{L}x) dx$    
  $\displaystyle = \frac{1}{2} \left[ \frac{L}{(m+n)\pi}{\mathrm {sen}}(\frac{m\pi... ...(m-n)\pi}{\mathrm {sen}}(\frac{m\pi}{L}x-\frac{n\pi}{L}x) \right]_{-L}^{L} = 0,$    

pois a função seno se anula para argumentos múltiplos inteiros de $\pi $. Da mesma forma, ainda para $m \neq n$,

$\displaystyle \int_{-L}^{L}$ $\displaystyle {\mathrm {sen}}(\frac{m\pi}{L}x) {\mathrm {sen}}(\frac{n\pi}{L}x) dx$    
  $\displaystyle = \frac{1}{2} \int_{-L}^{L} \cos(\frac{m\pi}{L}x-\frac{n\pi}{L}x) - \cos(\frac{m\pi}{L}x+\frac{n\pi}{L}x) dx$    
  $\displaystyle = \frac{1}{2} \left[ \frac{L}{(m-n)\pi}{\mathrm {sen}}(\frac{m\pi... ...(m+n)\pi}{\mathrm {sen}}(\frac{m\pi}{L}x+\frac{n\pi}{L}x) \right]_{-L}^{L} = 0,$    

e isto termina a prova. $\qedsymbol$

Em relação ao conjunto $\mathcal{F}$ do teorema anterior, é importante provar que o produto interno de uma destas funções com ela mesma não se anula. Faremos isto agora pois precisaremos destes resultados mais tarde. Usando as fórmulas para as integrais de seno e cosseno quadrado, obtidas na seção 4.2, temos

$\displaystyle \int_{-L}^{L} \cos(\frac{m\pi}{L}x) \cos(\frac{m\pi}{L}x) dx$ $\displaystyle = \int_{-L}^{L} \cos^{2}(\frac{m\pi}{L}x) dx$    
  $\displaystyle = \frac{L}{m\pi} \int_{-m\pi}^{m\pi} \cos^{2}u du$    
  $\displaystyle = \frac{L}{m\pi} \left[ \frac{1}{2}u + \frac{1}{4} {\mathrm {sen}}(2u) \right]_{-m\pi}^{m\pi} = L,$    

desde que $m \neq 0$. Se $m = 0$ então claramente

$\displaystyle \int_{-L}^{L} \cos(\frac{m\pi}{L}x) \cos(\frac{m\pi}{L}x) dx = \int_{-L}^{L} dx = 2L. $

Da mesma forma temos que

$\displaystyle \int_{-L}^{L} {\mathrm {sen}}(\frac{m\pi}{L}x) {\mathrm {sen}}(\frac{m\pi}{L}x) dx$ $\displaystyle = \int_{-L}^{L} {\mathrm {sen}}^{2}(\frac{m\pi}{L}x) dx$    
  $\displaystyle = \frac{L}{m\pi} \int_{-m\pi}^{m\pi} {\mathrm {sen}}^{2}u du$    
  $\displaystyle = \frac{L}{m\pi} \left[ \frac{1}{2}u - \frac{1}{4} {\mathrm {sen}}(2u) \right]_{-m\pi}^{m\pi} = L,$    

desde que $m \neq 0$. O caso $m = 0$ fica

$\displaystyle \int_{-L}^{L} {\mathrm {sen}}(\frac{m\pi}{L}x) {\mathrm {sen}}(\frac{m\pi}{L}x) dx = \int_{-L}^{L} 0 dx = 0. $

Vamos agora obter as expressões para os coeficientes $a_{k}$ e $b_{k}$, admitindo que a função $f$ possa ser escrita na forma da série (4.11), ou ainda,

$\displaystyle f(x) = a_{0} + \sum_{k=1}^{\infty} \left( a_{k}\cos(\frac{k\pi}{L}x) +b_{k}{\mathrm {sen}}(\frac{k\pi}{L}x) \right).$ (4.12)

Primeiramente vamos obter $a_{0}$. Integrando (4.12) em $x$, de $-L$ a $L$, obtemos

$\displaystyle \int_{-L}^{L} f(x) dx = \int_{-L}^{L} a_{0} + \sum_{k=1}^{\infty}... ... a_{k}\cos(\frac{k\pi}{L}x) +b_{k}{\mathrm {sen}}(\frac{k\pi}{L}x) \right) dx. $

Como o somatório acima converge uniformemente então podemos integrar termo a termo. Temos assim,

$\displaystyle \int_{-L}^{L} f(x) dx$ $\displaystyle = \int_{-L}^{L} a_{0} dx + \sum_{k=1}^{\infty} \left( a_{k} \int_... ...k\pi}{L}x) dx + b_{k} \int_{-L}^{L} {\mathrm {sen}}(\frac{k\pi}{L}x) dx \right)$    
  $\displaystyle = \int_{-L}^{L} a_{0} dx = 2La_{0},$    

já que as integrais trigonométricas do somatório se anulam. Temos portanto que

$\displaystyle a_{0} = \frac{1}{2L} \int_{-L}^{L} f(x) dx. $

Para obter cada um dos demais termos $a_{n}$, para $n=1,2,3,\dots$, tomamos o produto interno de (4.12) com a respectiva função $\cos(\frac{n\pi}{L}x)$. Temos então

$\displaystyle \int_{-L}^{L} f(x)\cos(\frac{n\pi}{L}x) dx$ $\displaystyle = \int_{-L}^{L} \left( a_{0} + \sum_{k=1}^{\infty} a_{k}\cos(\fra... ...i}{L}x) +b_{k}{\mathrm {sen}}(\frac{k\pi}{L}x) \right) \cos(\frac{n\pi}{L}x) dx$    
  $\displaystyle = \int_{-L}^{L} a_{0}\cos(\frac{n\pi}{L}x) dx + \sum_{k=1}^{\infty} a_{k} \int_{-L}^{L} \cos(\frac{k\pi}{L}x) \cos(\frac{n\pi}{L}x) dx$    
  $\displaystyle \qquad \qquad + \sum_{k=1}^{\infty} b_{k} \int_{-L}^{L} {\mathrm {sen}}(\frac{k\pi}{L}x) \cos(\frac{n\pi}{L}x) dx.$    

De acordo com os resultados do teorema 4.6, as integrais do último membro se anulam todas, exceto a integral em cossenos quando $k = n \neq 0$. Segue que

$\displaystyle \int_{-L}^{L} f(x)\cos(\frac{n\pi}{L}x) dx = a_{n} \int_{-L}^{L} \cos(\frac{n\pi}{L}x) \cos(\frac{n\pi}{L}x) dx = a_{n} L, $

e, portanto,

$\displaystyle a_{n} = \frac{1}{L} \int_{-L}^{L} f(x) \cos(\frac{n\pi}{L}x) dx, $

para todo $n=1,2,3,\dots$.

Analogamente obtemos cada um dos coeficientes $b_{n}$, tomando o produto interno de (4.12) com a respectiva função ${\mathrm {sen}}(\frac{n\pi}{L}x)$. Temos então que

$\displaystyle \int_{-L}^{L} f(x){\mathrm {sen}}(\frac{n\pi}{L}x) dx$ $\displaystyle = \int_{-L}^{L} a_{0}{\mathrm {sen}}(\frac{n\pi}{L}x) dx + \sum_{... ...} a_{k} \int_{-L}^{L} \cos(\frac{k\pi}{L}x) {\mathrm {sen}}(\frac{n\pi}{L}x) dx$    
  $\displaystyle \qquad \qquad + \sum_{k=1}^{\infty} b_{k} \int_{-L}^{L} {\mathrm {sen}}(\frac{k\pi}{L}x) {\mathrm {sen}}(\frac{n\pi}{L}x) dx.$    

De acordo com os resultados obtidos no teorema 4.6, as integrais do último membro se anulam todas, exceto a integral em senos quando $k = n \neq 0$. Temos assim,

$\displaystyle \int_{-L}^{L} f(x){\mathrm {sen}}(\frac{n\pi}{L}x) dx = b_{n} \in... ...{\mathrm {sen}}(\frac{n\pi}{L}x) {\mathrm {sen}}(\frac{n\pi}{L}x) dx = b_{n}L. $

Segue que

$\displaystyle b_{n} = \frac{1}{L} \int_{-L}^{L} f(x){\mathrm {sen}}(\frac{n\pi}{L}x) dx, $

para $n=1,2,3,\dots$.

Desta forma temos que

$\displaystyle f(x) = \frac{a_{0}}{2} + \sum_{k=1}^{\infty} a_{k}\cos(\frac{k\pi}{L}x) +b_{k}{\mathrm {sen}}(\frac{k\pi}{L}x)$ (4.13)

para

$\displaystyle a_{k} = \frac{1}{L} \int_{-L}^{L} f(x) \cos(\frac{k\pi}{L} x) dx \qquad (k \geq 0), $

e

$\displaystyle b_{k} = \frac{1}{L} \int_{-L}^{L} f(x) {\mathrm {sen}}(\frac{k\pi}{L} x) dx \qquad (k > 0), $

desde que $f$ admita representação na forma da série (4.11). O ajuste $\frac{1}{2}$ em $a_{0}$ é só para padronizar a expressão dos $a_{k}$ para todo $k \in \mathbb{N}$.

Os coeficientes $a_{k}$ e $b_{k}$ obtidos pelas expressões acima são chamados de coeficientes de Fourier da função $f$. A série em (4.13) é chamada de série de Fourier de $f$. Muito cuidado neste momento. A série do lado direito de (4.13) simplesmente é definida como sendo a série de Fourier da função $f$. Não falamos nada a respeito da série de Fourier de $f$ convergir para $f$, aliás, admitimos esta convergência para calcular os coeficientes. Isto significa que garantir a igualdade (4.13) é um pouco mais complicado do que parece.

Apresentamos agora um teorema que garante esta convergência. A demonstração pode ser encontrada em [3, Iorio] ou [2, Guidorizzi].

Teorema 4.7   Seja $f:[-L,L] \to \mathbb{R}$ uma função contínua, com derivada segunda contínua por partes e tal que $f(-L) = f(L)$. Então a série de Fourier de $f$ converge uniformemente para $f$ em $[-L,L]$. Isto é,
$\displaystyle f(x) = \frac{a_{0}}{2} + \sum_{k=1}^{\infty} \left[ a_{k} \cos(\frac{k\pi}{L}x) + b_{k} {\mathrm {sen}}(\frac{k\pi}{L}x) \right], $

para todo $x \in [-L,L]$.

A hipótese de que $f$ seja contínua é bastante forte. Na verdade, esta hipótese pode ser reduzida para uma hipótese de continuidade por partes. A hipótese de continuidade por partes da derivada segunda já garante isto. Neste caso, em cada ponto $x$ de continuidade de $f$ a série de Fourier de $f$ converge para $f$ e nos pontos de descontinuidade (descontinuidade tipo salto) a série de Fourier converge para o ponto médio dos limites laterais de $f$. Este resultado pode ser encontrado também em [3, Iorio].

Podemos também colocar o intervalo de interesse como sendo um intervalo da forma $[0,L]$. Isto não é problema pois dada uma função $f$ definida no intervalo $[0,L]$ podemos construir uma extensão $\overline{f}$ de $f$ a todo intervalo $[-L,L]$ por

$\displaystyle \overline{f}(x) = \left\{ \begin{array}{lcl} 0 & \text{se} & -L \leq x < 0 \\ f(x) & \text{se} & 0 \leq x \leq L, \end{array} \right. $

e os coeficientes $a_{k}$ e $b_{k}$ de $\bar{f}$ ficam também reduzidos a

$\displaystyle a_{k} = \frac{1}{L} \int_{-L}^{L} \overline{f}(x) \cos(\frac{k\pi}{L} x) dx = \frac{1}{L} \int_{0}^{L} f(x) \cos(\frac{k\pi}{L} x) dx, $

e

$\displaystyle b_{k} = \frac{1}{L} \int_{-L}^{L} \overline{f}(x) {\mathrm {sen}}... ...L} x) dx = \frac{1}{L} \int_{0}^{L} f(x) {\mathrm {sen}}(\frac{k\pi}{L} x) dx, $

que são na verdade coeficientes para $f$ restritos ao intervalo $[0,L]$.

Embora a série de Taylor desempenha um papel fundamental para a matemática aplicada, a série de Fourier apresenta propriedades que a tornam mais adequada para certas aplicações. Dentre estas propriedades, um fato relevante é que os coeficientes da série de Taylor são os termos $\frac{f^{(n)}(x_{0})}{n!}$ e então a função $f$ deve possuir derivadas de ordem $n$ contínuas no ponto $x_{0}$. A série de Fourier não exige tanto. O teorema que apresentamos exige apenas derivada segunda contínua por partes.

Além disso, a série de Taylor é uma série com boa aproximação para a função nas proximidades do ponto $x_{0}$. Quanto mais afastado do ponto $x_{0}$ mais coeficientes serão necessários para uma aproximação satisfatória. Já a série de Fourier tem comportamento global. Isto significa que não é necessário aumentar o número de coeficientes quando se muda o ponto de interesse do intervalo $[-L,L]$.

Uma aplicação prática do uso da série de Fourier é o armazenamento e transmissão de imagens. Consideremos que uma fotografia seja tirada em um telefone celular com câmera. A foto é composta de pontos coloridos. Supondo que a resolução da foto seja de $640 \times 480$, então a foto é um retângulo de 640 pontos de largura por 480 pontos de altura. São portanto 307.200 pontos coloridos, dispostos em 640 colunas e 480 linhas.

Para gravar esta foto, no sistema VGA, são armazenados 3 bytes de informações para cada um destes pontos. Estes bytes correspondem às intensidades de vermelho, verde e azul de cada ponto. São então 921.600 bytes que devem ser gravados, isto sem contar outras informações, conhecidas como o cabeçalho da imagem. Cada byte armazena como informação um número inteiro de 0 a 255.

Vamos agora ver como a série de Fourier pode ajudar a economizar espaço para gravar esta figura.

Se olharmos para cada uma das 480 linhas que compõem a figura temos que cada linha possui 640 pontos. São 640 bytes armazenando as intensidades de vermelho, 640 armazenando as intensidades de verde e 640 as intensidades de azul, num total de 1.920 bytes para cada uma das 480 linhas da figura. Se traçarmos um gráfico destes 640 valores para a intensidade de vermelho, podemos construir uma função $f(x)$ que representa estas intensidades.

A função será portanto uma função constante em cada um dos 640 subintervalos no qual foi dividido o intervalo $[0,L] = [0,640]$.

Figura 4.3: Gráfico de uma cor de uma linha da figura.
Image SFcor

A função pode ainda ser reescalonada para que os valores estejam, digamos de 0 a 1, ao invéz de 0 a 255. O reescalonamento é para que os saltos da função sejam pequenos, diminuindo a oscilação da série de Fourier na passagem de um segmento a outro.

Feito isto, montamos a série de Fourier desta função $f$. A série de Fourier de $f$ dará uma boa aproximação para a função $f$. Tudo o que precisamos armazenar agora são os coeficientes de Fourier desta série. Exemplificaremos o processo considerando 21 coeficientes, sendo eles $a_{0}$, $a_{n}$ e $b_{n}$ para $n = 1, 2, \dots, 10$. Como estes coeficientes são números reais, então o armazenamento de cada um destes números ocupa 6 bytes, totalizando 126 bytes para os 21 coeficientes de Fourier.

Desta forma, ao invés de gastar 640 bytes para armazenar as intensidades de vermelho, podemos usar apenas 126 bytes. Repetindo este processo para as intensidades de verde e de azul, temos o armazenamento de 378 bytes para cada linha da figura, no lugar dos 1.920 bytes tradicionais.

Aplicando isto a todas as 480 linhas da figura, temos um gasto de 181.440 bytes ao invés dos 921.600 tradicionais. Uma compactação de mais de 80%. Levemos ainda em conta que podem ser armazenados mais do que os 21 coeficientes que citamos, ou menos. Gravando mais coeficientes implicará em uma maior qualidade da imagem, porém, menos economia de espaço e menos coeficientes implicarão menor qualidade, porém, maior economia de espaço. Pode-se ainda trabalhar com apenas os coeficientes da função seno ou somente com os coeficientes da função cosseno. O formato de imagens conhecido como JPG ou JPEG é um sistema de compressão e armazenamento de imagens baseado em uma série de cossenos.

O espaço necessário para gravar uma figura já não é um grande problema. Os atuais discos rígidos e os cartões de memória para celulares e câmeras digitais já possuem uma capacidade de armazenamento bem expressiva, o que poderia até dispensar uma compactação da imagem. Mas a transmissão das imagens é ainda um problema.

Celulares com tecnologia GSM transmitem dados a uma taxa máxima de 9.600bps, isto é, 9.600 bits por segundo e isto significa 1.200 bytes por segundo (1byte = 8bits). A tecnologia GPRS possui na prática uma taxa de transmissão de dados de até 40.200bps (em teoria até 171.200bps). A tecnologia EDGE transmite na prática até 384.000bps (em teoria até 473.600bps). A tecnologia 3G transmite até 7Mbps (Mega bits por segundo), isto é, 7.340.032 bits por segundo, ou 917.504 bytes por segundo.

Uma imagem com 921.600 bytes necessita de 768 segundos, ou 12 minutos e 48 segundos para a transmissão via GSM. Já uma imagem de 181.440 bytes, compactada por série de Fourier, necessita de 152 segundos, ou 2 minutos e 32 segundos para a transmissão. Isto conseguindo a taxa máxima de transmissão. Independentemente da tecnologia utilizada ou da taxa de transmissão atingida, 921.600 bytes sempre necessitarão 5 vezes mais tempo para serem transmitidos do que 181.440 bytes.

A evolução das tecnologias de celulares ajuda na redução do tempo de transmissão. Na contramão desta evolução, a resolução das imagens também evolui. Resoluções maiores como $800 \times 600$ ou $1.280 \times 960$, significam que as imagens possuem mais pontos e, consequentemente, exigem mais espaço para a gravação e mais tempo para a transmissão. A compactação continua sendo importante neste processo pois diminui o tamanho e o tempo de transmissão das imagens, quaisquer que sejam as tecnologias utilizadas para armazenamento e transmissão de dados.

4.5 Lançamento vertical e queda livre com resistência

Nesta seção vamos estudar a velocidade de um objeto lançado verticalmente para cima, em determinado momento $t_{0}$, a uma certa velocidade inicial $v_{0}$. Quando este objeto atingir a altura máxima, ele começa a cair. Vamos também estudar esta velocidade de queda.

Consideremos um sistema coordenado com apenas um eixo vertical, apontando para cima, cuja origem é o nível do solo. Designemos por $t$ o tempo, $y(t)$ a posição (altura em relação ao solo) do objeto e $v(t)$ a velocidade do objeto no instante $t$.

Supondo que este objeto seja então lançado para cima, ele está sujeito à ação da gravidade e também a uma força de atrito com o ar. Em geral, forças de atrito são consideradas como sendo proporcionais a uma potência da velocidade. Esta potência varia de acordo com a própria velocidade. Para problemas desta natureza a potência considerada é 2.

A ação da gravidade resume-se na força peso $p = -mg$, sendo $m$ a massa do objeto e $g$ a aceleração da gravidade. A força de atrito $r$ com o ar, é considerada como $r = -kv^{2}$, sendo $k>0$ a constante de proporcionalidade que é dependente de alguns fatores como densidade do ar e a área da secção transversal frontal do objeto. O sinal negativo das duas forças é decorrente do fato que são contrárias ao referencial, isto é, ambas apontam para baixo.

Para um corpo qualquer, a constante de proporcionalidade é dada por $k = \frac{\rho A \delta}{2}$, sendo que $\rho$ é a densidade do ar, $A$ é a área da secção transversal frontal exposta ao ar e $\delta$ é um coeficiente que depende da forma do objeto. Embora a densidade do ar varie com a altura, para cálculos aproximados em baixa altitude, pode ser utilizado o valor ao nível do mar que é de $1,29 Kg/m^{3}$.

De acordo com a segunda lei de Newton, temos que $F = ma$, sendo $F$ a força resultante do sistema, que é a soma das duas forças consideradas. Temos assim,

$\displaystyle ma = F = p + r = -mg - kv^{2}. $

A aceleração $a$ por sua vez é igual à derivada da velocidade em função do tempo e então temos

$\displaystyle m v' = ma = -mg - kv^{2}. $

Esta é uma equação diferencial não linear, sujeita a uma condição inicial $v(t_{0}) = v_{0}$. Resolver esta equação nos fornece $v(t)$ que é a velocidade do objeto em função do tempo. Vamos obter esta solução. Reescrevemos a equação diferencial na forma

$\displaystyle v' = -g(1 + \frac{k}{mg}v^{2}), $

ou, ainda,

$\displaystyle \frac{v'}{(1 + \frac{k}{mg}v^{2})} = -g. $

Para simplificar, chamemos $\lambda^{2} = \frac{k}{mg}$ e integrando a equação anterior em $t$, temos

$\displaystyle \int \frac{v'}{(1 + \lambda^{2}v^{2})} dt = -gt + C, $

para algum $C \in \mathbb{R}$, constante de integração.

A integral do primeiro membro pode ser determinada por

$\displaystyle \int \frac{v'}{(1 + \lambda^{2}v^{2})} dt$ $\displaystyle = \int \frac{\frac{dv}{dt}}{(1 + \lambda^{2}v^{2})} dt$    
  $\displaystyle = \int \frac{1}{(1 + \lambda^{2}v^{2})} dv = \frac{1}{\lambda} {\mathrm {tg}}^{-1}(\lambda v),$    

donde segue que

$\displaystyle {\mathrm {tg}}^{-1}(\lambda v) = -\lambda gt + C, $

para alguma constante de integração $C$. Usando a condição inicial $v(t_{0}) = v_{0}$, temos

$\displaystyle C = {\mathrm {tg}}^{-1}(\lambda v_{0}) + \lambda gt_{0}. $

Temos portanto que a velocidade $v$ é dada implicitamente por

$\displaystyle {\mathrm {tg}}^{-1}(\lambda v)$ $\displaystyle = -\lambda gt + {\mathrm {tg}}^{-1}(\lambda v_{0}) + \lambda gt_{0},$    
  $\displaystyle = {\mathrm {tg}}^{-1}(\lambda v_{0}) - \lambda g(t-t_{0}).$    

Aplicando tangente em ambos os membros e usando a identidade da soma de arcos para a tangente, temos

$\displaystyle \lambda v = \lambda v(t)$ $\displaystyle = {\mathrm {tg}}( {\mathrm {tg}}^{-1}(\lambda v_{0})-\lambda g(t-t_{0}) )$    
  $\displaystyle = \frac{\lambda v_{0} - {\mathrm {tg}}(\lambda g(t-t_{0}))}{1 + \lambda v_{0}{\mathrm {tg}}(\lambda g(t-t_{0}))},$ (4.14)

para qualquer $t > t_{0}$.

O movimento de ascendência do objeto é então dado em termos da função tangente. Sabemos que este movimento deve obrigatoriamente cessar na ausência de outras forças. Para ser mais preciso, observe que conforme $t$ cresce, a equação (4.14) nos diz que $v$ decresce. Como a função tangente vai para o infinito continuamente quando o argumento se aproxima de $\frac{\pi}{2}$, então existe um tempo $t_{1} > t_{0}$ de forma que o numerador de (4.14) se anula.

Este tempo $t_{1}$, é o tempo em que o objeto atinge a velocidade $v(t_{1}) = 0$ e começa o movimento de queda livre, de volta ao solo. Colocando $\lambda v_{0} - {\mathrm {tg}}(\lambda g(t_{1}-t_{0})) = 0$, podemos facilmente verificar que

$\displaystyle t_{1} = \frac{1}{\lambda g} {\mathrm {tg}}^{-1}(\lambda v_{0}) + t_{0}. $

A altura $y(t_{1})$ que o objeto atinge, antes de começar a cair, também pode ser determinada. Como sabemos, a velocidade $v(t)$ do objeto, é dada em termos da sua posição $y(t)$ pela igualdade

$\displaystyle v(t) = \frac{dy}{dt}, $

e portanto

$\displaystyle y(t) = \int v(t) dt + C, $

para alguma constante de integração $C$. Substituindo $v(t)$ temos

$\displaystyle y(t) = \int \frac{1}{\lambda} {\mathrm {tg}}( {\mathrm {tg}}^{-1}(\lambda v_{0})-\lambda g(t-t_{0}) ) dt + C, $

e fazendo a mudança de variáveis $s = {\mathrm {tg}}^{-1}(\lambda v_{0})-\lambda g(t-t_{0})$, temos $\frac{ds}{dt} = -\lambda g$, e assim

$\displaystyle y(t)$ $\displaystyle = \frac{1}{\lambda} \int {\mathrm {tg}}( {\mathrm {tg}}^{-1}(\lambda v_{0})-\lambda g(t-t_{0}) ) dt + C$    
  $\displaystyle = \frac{-1}{\lambda^{2}g} \int {\mathrm {tg}}s ds + C$    
  $\displaystyle = \frac{-1}{\lambda^{2}g} \int \frac{{\mathrm {sen}}s}{\cos s} ds + C = \frac{-1}{\lambda^{2}g} \ln\vert\cos s\vert + C.$    

Observe que nesta etapa, estamos considerando que $t_{0} \leq t \leq t_{1}$. Nestes termos,

$\displaystyle 0 < \lambda g(t-t_{0}) < \lambda g(t_{1}-t_{0}), $

e lembrando que $\lambda g(t_{1}-t_{0}) = {\mathrm {tg}}^{-1}(\lambda v_{0})$, temos que

$\displaystyle 0 < {\mathrm {tg}}^{-1}(\lambda v_{0}) - \lambda g(t-t_{0}) < {\mathrm {tg}}^{-1}(\lambda v_{0}) < \frac{\pi}{2}. $

Isto significa que $0 < s < \frac{\pi}{2}$ e neste intervalo temos que $\cos s > 0$. Podemos portanto descartar o módulo no logaritmo. Segue que

$\displaystyle y$ $\displaystyle = \frac{-1}{\lambda^{2}g} \ln(\cos s) + C$    
  $\displaystyle = \frac{-1}{\lambda^{2}g} \ln\left( \cos( {\mathrm {tg}}^{-1}(\lambda v_{0})-\lambda g(t-t_{0}) ) \right)+ C,$    

para alguma constante de integração $C$. Para determinar a constante $C$, usamos a condição inicial $y(t_{0}) = 0$, que nos fornece $C = \frac{1}{\lambda^{2}g} \ln\left( \cos\left( {\mathrm {tg}}^{-1}(\lambda v_{0}) \right) \right)$. Temos assim, que a altura do objeto em um determinado tempo $t$ com $t_{0} \leq t \leq t_{1}$, é dada por

$\displaystyle y(t) = \frac{-1}{\lambda^{2}g} \ln\left( \cos( {\mathrm {tg}}^{-1... ...1}{\lambda^{2}g} \ln\left( \cos( {\mathrm {tg}}^{-1}(\lambda v_{0}) ) \right), $

sendo portanto a altura máxima que o objeto atinge

$\displaystyle y(t_{1}) = \frac{1}{\lambda^{2}g} \ln\left( \cos( {\mathrm {tg}}^{-1}(\lambda v_{0}) ) \right). $

Agora, vamos seguir o estudo quando $t > t_{1}$. No instante $t_{1}$, o objeto atinge a altura máxima e começa então o movimento de descida do objeto conhecido como movimento de queda livre. O problema da queda livre pode ser totalmente desvinculado do que esquematizamos até agora. Um objeto pode cair em queda livre sem ter sido necessariamente arremessado para cima. Um exemplo disto é um paraquedista que salta de um avião.

A equação de descida do objeto é um pouco diferente pois agora a força de atrito age no mesmo sentido do referencial. A equação das forças é agora dada por

$\displaystyle ma = F = p + r = -mg + kv^{2}, $

e, portanto, a equação diferencial é dada por

$\displaystyle v' = a = g\left( \tfrac{k}{gm}v^{2} - 1 \right) = g(\lambda^{2}v^{2}-1),$ (4.15)

sujeita à condição inicial $v(t_{1}) = v_{1}$. No caso do corpo ser arremessado verticalmente para cima, temos que $v(t_{1}) = v_{1} = 0$. Por uma questão de simplicidade substituímos o termo $\frac{k}{gm}$ por $\lambda^{2}$.

Temos portanto um problema de valor inicial

$\displaystyle \left\{ \begin{array}{l} v' = g(\lambda^{2}v^{2}-1) \\ v(t_{1}) = v_{1}. \end{array} \right. $

Reescrevendo a equação diferencial obtemos

$\displaystyle \frac{1}{(\lambda^{2}v^{2}-1)} v' = g, $

e integrando em $t$, com a mudança de variáveis $u =\lambda v$, temos

$\displaystyle gt = \int \frac{1}{\lambda^{2}v^{2}-1} v' dt = \int \frac{1}{\lambda^{2}v^{2}-1} dv = -\frac{1}{\lambda} \int \frac{1}{1-u^{2}} du. $

De acordo com as fórmulas de derivação para as funções trigonométricas hiperbólicas inversas (ver tabela 3.1) temos que a integral do último membro é igual a ${\mathrm {tgh}}^{-1} u$ para $u \in (-1,1)$, ou igual a ${\mathrm{ctgh}}^{-1} u$ se $u \in (-\infty,-1) \cup (1,\infty)$.

Observemos que não há a possibilidade de que $u = \lambda v = \pm 1$, em virtude de que a força de aceleração $v'$ nunca se anula (a menos que não haja gravidade) e, portanto, o lado direito da igualdade (4.15) também nunca se anula.

Resta que ou $\lambda^{2} v^{2} > 1$ ou $\lambda^{2} v^{2} < 1$. Isto será uma decorrência da velocidade inicial de queda $v_{1}$. Se $v_{1}^{2} = ( v(t_{1}) )^{2} > \frac{1}{\lambda^{2}}$ então esta desigualdade se mantem para todo $t > t_{1}$ e se $v_{1}^{2} < \frac{1}{\lambda^{2}}$ então isto se mantem para todo $t > t_{1}$.

Para não sobrecarregar (ainda mais) o texto, vamos escolher uma das duas situações observadas acima. Para ficar consistente com início da seção, isto é, o arremesso vertical e o instante $t_{1}$ no qual $v_{1} = v(t_{1}) = 0$, escolhemos o caso em que $\lambda^{2} v^{2} < 1$. Assumindo esta condição, temos que $u = \lambda v \in (-1,1)$ e a solução da equação diferencial será dada implicitamente por

$\displaystyle gt = -\frac{1}{\lambda} \int \frac{1}{1-u^{2}} du = -\frac{1}{\lambda} {\mathrm {tgh}}^{-1} u + C, $

e voltando à variável $v$,

$\displaystyle \lambda gt = -{\mathrm {tgh}}^{-1}(\lambda v) + C. $

A constante $C$, calculada pela condição inicial $v(t_{1}) = v_{1}$, é

$\displaystyle C = \lambda g t_{1} + {\mathrm {tgh}}^{-1}(\lambda v_{1}), $

o que nos leva a

$\displaystyle \lambda gt = -{\mathrm {tgh}}^{-1}(\lambda v) + \lambda g t_{1} + {\mathrm {tgh}}^{-1}(\lambda v_{1}). $

Com o intuito de isolar a velocidade $v$, reescrevemos a igualdade na forma

$\displaystyle {\mathrm {tgh}}^{-1}(\lambda v) = {\mathrm {tgh}}^{-1}(\lambda v_{1}) - \lambda g(t-t_{1}), $

e aplicamos tangente hiperbólica em ambos os membros, obtendo

$\displaystyle \lambda v = {\mathrm {tgh}}({\mathrm {tgh}}^{-1}(\lambda v_{1}) -... ...gh}}(\lambda g(t-t_{1}))}{1-\lambda v_{1}{\mathrm {tgh}}(\lambda g(t-t_{1}))}. $

A velocidade de queda do objeto é dada portanto em termos da função tangente hiperbólica. Vamos analisar o comportamento da velocidade $v$ quando $t \to \infty$. Observe que na prática não podemos considerar $t \to \infty$, porque certamente o objeto atinge o solo em um tempo finito. Mas esta análise nos trará boas ideias sobre a velocidade terminal, isto é, a velocidade aproximada com que o objeto atinge o solo.

Lembremos que ${\mathrm {tgh}}u \to 1$, quando $u \to \infty$ (Ver seção 2.3). Assim, quando $t \to \infty$, temos

$\displaystyle \lambda v = \frac{\lambda v_{1} - {\mathrm {tgh}}(2\lambda g(t-t_... ...gh}}(2\lambda g(t-t_{1}))} \to \frac{\lambda v_{1} - 1}{1-\lambda v_{1}} = -1, $

donde $v \to -\frac{1}{\lambda} = -\sqrt{\frac{mg}{k}}$. O sinal negativo decorre do fato de que a velocidade do objeto é um vetor que aponta em sentido contrário ao referencial escolhido.

Supondo que o objeto em questão fosse um paraquedista com paraquedas aberto, temos que a velocidade terminal do paraquedista (em módulo) é $v_{t} = \frac{1}{\lambda} = \sqrt{\frac{mg}{k}} = \sqrt{\frac{2p}{\rho A\delta}}$, sendo $p$ o peso do paraquedista, $\rho$ a densidade do ar e $A$ a área do paraquedas.

Vemos então que quanto maior for o peso do paraquedista, maior a velocidade terminal. Também, quanto maiores forem a área do paraquedas ou a densidade do ar, menor a velocidade terminal.

Podemos também determinar o tempo $t_{2}$ que o objeto leva para atingir o solo novamente. Este tempo é exatamente o tempo em que $y(t_{2}) = 0$. O problema momentâneo é que não temos ainda uma identidade para a posição $y$ do objeto, no momento de queda. Vamos determinar esta igualdade. Como feito anteriormente

$\displaystyle y(t) = \int v(t) dt + C, $

para alguma constante de integração $C$, que será determinada pela condição inicial $y(t_{1}) = h$ a altura em que o objeto foi solto em queda livre no instante $t_{1}$. No caso de o objeto ter sido arremessado verticalmente, então lembremos que esta condição será $y(t_{t}) = h = \frac{1}{\lambda^{2}g} \ln\left( \cos( {\mathrm {tg}}^{-1}(\lambda v_{0}) ) \right)$.

Substituindo $v(t)$ na equação integral, temos

$\displaystyle y(t) = \frac{1}{\lambda} \int {\mathrm {tgh}}({\mathrm {tgh}}^{-1}(\lambda v_{1}) - \lambda g(t-t_{1})) dt + C, $

e fazendo a mudança de variáveis $s = {\mathrm {tgh}}^{-1}(\lambda v_{1}) - \lambda g(t-t_{1})$, temos $\frac{ds}{dt} = -\lambda g$ e, assim,

$\displaystyle y(t)$ $\displaystyle = -\frac{1}{\lambda^{2}g} \int {\mathrm {tgh}}s ds + C$    
  $\displaystyle = -\frac{1}{\lambda^{2}g} \int \frac{{\mathrm{senh}}s}{\cosh s} ds + C$    
  $\displaystyle = -\frac{1}{\lambda^{2}g} \ln( \cosh s )+ C$    
  $\displaystyle = -\frac{1}{\lambda^{2}g} \ln\left(\cosh( {\mathrm {tgh}}^{-1}(\lambda v_{1}) - \lambda g(t-t_{1}) ) \right) + C.$    

Substituindo a condição $y(t_{1}) = h$, temos

$\displaystyle C = h + \frac{1}{\lambda^{2}g} \ln \cosh( {\mathrm {tgh}}^{-1}(\lambda v_{1}) ), $

e, assim,

$\displaystyle y(t) = h + \frac{1}{\lambda^{2}g} \ln\left(\cosh( {\mathrm {tgh}}... ...eft(\cosh( {\mathrm {tgh}}^{-1}(\lambda v_{1}) - \lambda g(t-t_{1}) ) \right). $

Reorganizando temos que

$\displaystyle \lambda^{2} gy$ $\displaystyle = \lambda^{2}gh + \ln\frac{\cosh({\mathrm {tgh}}^{-1}(\lambda v_{1}))}{\cosh({\mathrm {tgh}}^{-1}(\lambda v_{1})-\lambda g(t-t_{1}))}$    
  $\displaystyle = \lambda^{2}gh - \ln\frac{\cosh({\mathrm {tgh}}^{-1}(\lambda v_{1})-\lambda g(t-t_{1}))}{\cosh({\mathrm {tgh}}^{-1}(\lambda v_{1}))},$    

e calculando o tempo $t_{2}$, para que $y(t_{2}) = 0$, temos

$\displaystyle t_{2} = t_{1} + \frac{1}{\lambda g}\left({\mathrm {tgh}}^{-1}(\la... ...^{\lambda^{2}gh} \cosh({\mathrm {tgh}}^{-1}(\lambda v_{1})) \right) \right). $

Para finalizar, observamos que se tivéssemos escolhido $\lambda^{2} v_{1}^{2} > 1$, então a velocidade seria dada por

$\displaystyle \lambda v$ $\displaystyle = {\mathrm{ctgh}}( {\mathrm{ctgh}}^{-1}(\lambda v_{1}) -\lambda g(t-t_{1}) )$    
  $\displaystyle = \frac{1-{\mathrm {tgh}}({\mathrm{ctgh}}^{-1}(\lambda v_{1})) {\... ...h}}({\mathrm{ctgh}}^{-1}(\lambda v_{1})) - {\mathrm {tgh}}(\lambda g(t-t_{1}))}$    
  $\displaystyle = \frac{1- \frac{1}{\lambda v_{1}} {\mathrm {tgh}}(\lambda g(t-t_... ...(\lambda g(t-t_{1})) }{ 1 - \lambda v_{1} {\mathrm {tgh}}(\lambda g(t-t_{1}))},$    

e sabendo que ${\mathrm {tgh}}u \to 1$ quando $u \to \infty$, ainda teríamos $v \to -\frac{1}{\lambda} = -\sqrt{\frac{mg}{k}}$ quando $t \to \infty$.

4.6 O pêndulo simples

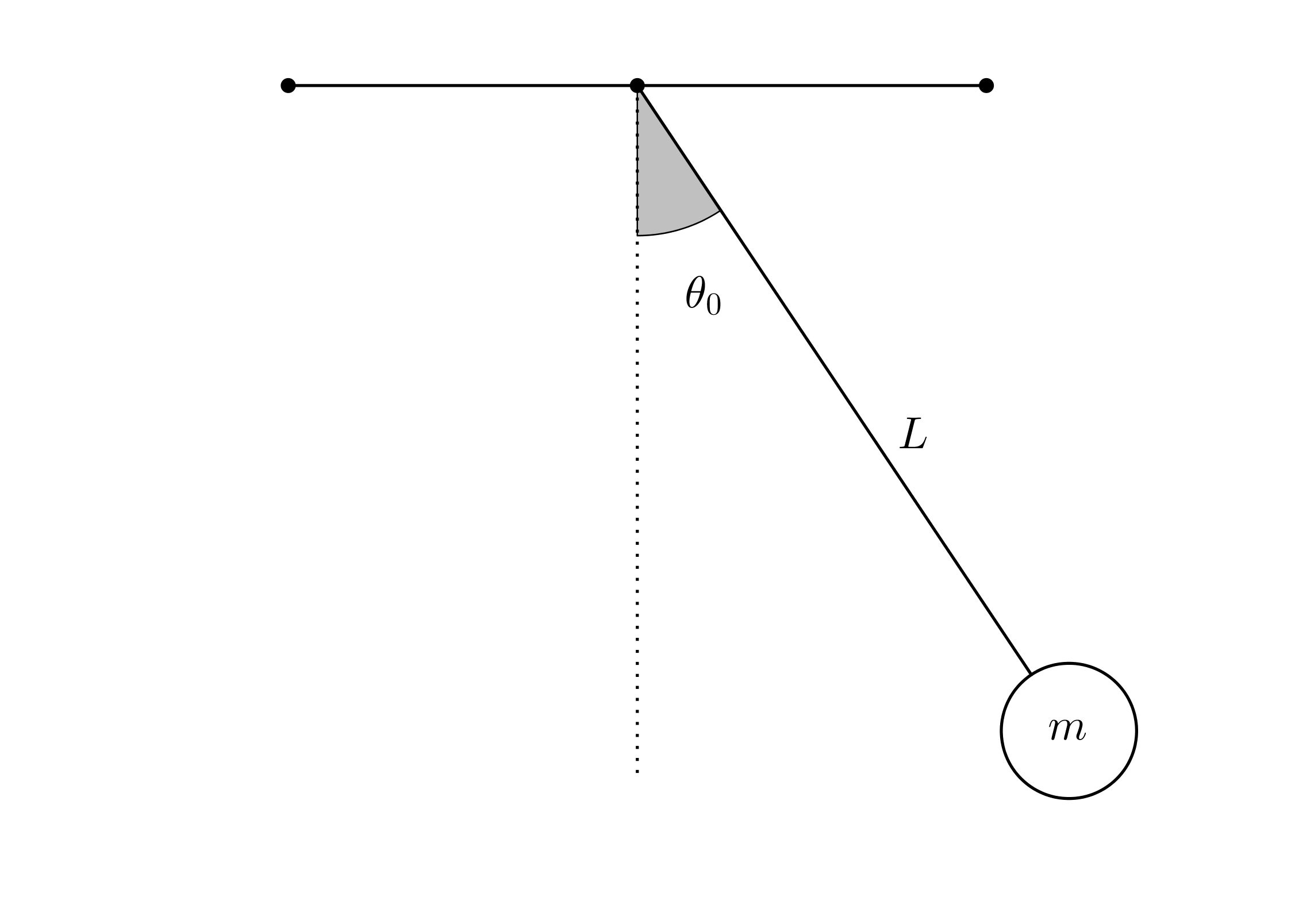
Um pêndulo consiste de um objeto de massa $m$ preso a um suporte horizontal rígido por um fio de comprimento $L$. O fio é considerado rígido, inextensível e com massa desprezível. Este objeto é solto de uma posição inicial, onde o fio faz um ângulo $\theta_{0}$ com a perpendicular e começa a oscilar em movimento de vai-e-vem. Vamos considerar que $\theta_{0} > 0$.

Uma vez solto o pêndulo, o ângulo $\theta$ que o fio faz com a perpendicular, varia com o tempo. Nestes termos $\theta$ é uma função da variável temporal $t$, isto é, $\theta = \theta(t)$ e, além disso, $-\theta_{0} < \theta < \theta_{0}$. A situação pode ser visualizada na figura 4.4.

Figura 4.4: Pêndulo simples.
Image pendulo

O movimento do objeto se dá em um plano bidimensional e descreve neste plano uma trajetória circular. Fixemos um sistema coordenado bidimensional nas coordenadas tangencial e radial ao movimento circular. Isto é, um dos eixos é tangente à trajetória circular enquanto o outro eixo é normal (perpendicular) à trajetória circular.

Sobre este objeto agem a força peso $\vec{p}$, a força $\vec{t}$ de tensão com a haste e uma força $\vec{r}$ de atrito (ou resistência do ar).

A força peso é decomposta, em termos do ângulo que a haste faz com a vertical, nas componentes tangencial e radial como $\vec{p} = (-mg {\mathrm {sen}}\theta, -mg \cos \theta)$, sendo $m$ a massa do objeto e $g$ a aceleração gravitacional.

A força de tensão com a haste é decomposta como $\vec{t} = (0,T)$ sendo $T$ o módulo da força de tensão na componente radial. A primeira coordenada é nula pois não há força de tensão com a haste no sentido tangencial.

Como a velocidade do pêndulo é pequena, a força de atrito $\vec{r}$ é considerada como sendo proporcional à velocidade $v$, isto é, $\vec{r} = (-kv,0)$, para uma constante de proporcionalidade $k>0$. O sinal negativo é consequência de que a força de atrito age no sentido contrário à velocidade. A segunda componente é nula pois a resistência não afeta o movimento radial. Na verdade, como a haste é considerada inextensível, não há movimento radial. A velocidade ainda deve ser dada em termos do deslocamento circular, isto é, $v = L \frac{d\theta}{dt}$.

Como vimos na seção anterior, $k = \frac{\rho A \delta}{2}$, em que $\rho$ é a densidade do ar, $A$ a área frontal do objeto e $\delta$ um coeficiente que depende da forma do objeto. Para objetos esféricos considera-se $\delta = \frac{1}{2}$.

De acordo com a segunda lei de Newton, temos $m\vec{a} = \vec{F}$, sendo que $\vec{F}$ é a força resultante do sistema. A aceleração $\vec{a}$ deve ser considerada somente na componente tangencial, em termos do deslocamento circular $\theta$. Isto é, $\vec{a} = \left( \frac{dv}{dt}, 0 \right) = \left( L \frac{d^{2}\theta}{dt^{2}}, 0 \right)$.

Assim, temos

$\displaystyle \left( mL \frac{d^{2}\theta}{dt^{2}}, 0 \right)$ $\displaystyle = m\vec{a} = \vec{F} = \vec{p}+\vec{t}+\vec{r}$    
  $\displaystyle = (-mg {\mathrm {sen}}\theta, -mg \cos \theta) + (0,T) + (-kv,0)$    
  $\displaystyle = \left( -mg {\mathrm {sen}}\theta - kL\tfrac{d\theta}{dt}, -mg \cos \theta + T \right).$    

Igualando cada uma das componentes temos que

  $\displaystyle mL\theta'' + kL \theta' + mg {\mathrm {sen}}\theta = 0,$ (4.16)
  $\displaystyle T = mg \cos \theta,$ (4.17)

sendo que $\theta' = \frac{d\theta}{dt}$. Este sistema está sujeito às condições iniciais em $t_{0}$, dadas por $\theta(t_{0}) = \theta_{0}$ o ângulo inicial em que o pêndulo é solto e $\theta'(t_{0}) = v_{0}$ a velocidade inicial do pêndulo. Se o pêndulo for solto do repouso, então naturalmente $\theta'(t_{0}) = v_{0} = 0$.

A equação (4.16) é uma equação diferencial não linear na variável $\theta = \theta(t)$. Garantir a existência de uma solução pode ser complicado e mais complicado ainda talvez seja encontrar esta solução. Modificações podem ser feitas na equação (4.16) a fim de facilitar a determinação de uma solução. Vamos estudar agora o caso em que a equação é liearizada, pois equações diferenciais lineares são mais fáceis de se obter solução. Vamos considerar então que o pêndulo oscile com variações pequenas do ângulo $\theta$. O limite (ver proposição 1.6),

$\displaystyle \lim_{\theta \to 0} \frac{{\mathrm {sen}}\theta}{\theta} = 1, $

sugere que para valores pequenos do argumento $\theta$, o numerador e o denominador são valores muito próximos. Podemos traduzir isto escrevendo ${\mathrm {sen}}\theta \approx \theta$ para valores pequenos de $\theta$. Para se ter uma ideia desta aproximação, o erro cometido ao aproximar ${\mathrm {sen}}\theta$ por $\theta$ para um ângulo de $10^{\circ}$, é menor que um milésimo.

Nesta abordagem, o termo não linear ${\mathrm {sen}}\theta$ é substituído por $\theta$ e a equação (4.16) torna-se

$\displaystyle mL\theta'' + kL \theta' + mg \theta = 0,$ (4.18)

que agora é uma equação diferencial linear. Esta equação diferencial possui soluções baseadas nas raízes da equação do segundo grau,

$\displaystyle mLx^{2} + kLx + mg = 0, $

chamada de equação auxiliar. A respeito destas raízes, temos três casos a considerar.

Caso 1. Se $\Delta = (k^{2}L^{2}-4m^{2}Lg) > 0$ então a equação auxiliar possui duas raízes reais distintas

$\displaystyle x_{1} = \frac{-kL + \sqrt{k^{2}L^{2}-4m^{2}Lg}}{2mL}, \qquad x_{2} = \frac{-kL - \sqrt{k^{2}L^{2}-4m^{2}Lg}}{2mL}, $

e a solução de (4.18) é da forma

$\displaystyle \theta = \theta(t) = C_{1}e^{x_{1}t} + C_{2}e^{x_{2}t}, $

para $C_{1}$ e $C_{2}$ constantes a serem determinadas pelas condições iniciais $y(0) = \theta_{0}$ e $y'(0) = v_{0}$.

Mas note que

$\displaystyle x_{1}$ $\displaystyle = \frac{-kL + \sqrt{k^{2}L^{2}-4m^{2}Lg}}{2mL} < \frac{-kL + \sqrt{k^{2}L^{2}}}{2mL} = 0$    
$\displaystyle x_{2}$ $\displaystyle = \frac{-kL - \sqrt{k^{2}L^{2}-4m^{2}Lg}}{2mL} < 0$    

e, portanto, o movimento angular do pêndulo decai a zero exponencialmente. Isto deve-se a um valor elevado da constante de proporcionalidade $k = \frac{\rho A \delta}{2}$. Valor alto o suficiente para tornar $k^{2}L^{2} > 4m^{2}Lg$. Observemos que se a densidade $\rho$, do meio em que o pêndulo estiver imerso for alta, então esta situação é atingida.

Neste caso, se o pêndulo passar pela solução de equilíbrio $\theta(t) = 0$, isto somente poderá ocorrer uma vez, exatamente no ponto

$\displaystyle t = \frac{mL}{\sqrt{k^{2}L^{2}-4m^{2}Lg}} \ln \left( -\frac{C_{2}}{C_{1}} \right), $

e somente se $C_{2}$ e $C_{1}$ possuírem sinais contrários.

Caso 2. Se $\Delta = (k^{2}L^{2}-4m^{2}Lg) = 0$, então a única raiz real da equação auxiliar é,

$\displaystyle x = \frac{-kL}{2mL} = \frac{-k}{2m}, $

e, neste caso, a solução de (4.18) é dada por

$\displaystyle \theta = \theta(t) = C_{1}e^{\frac{-k}{2m}t} + C_{2}te^{\frac{-k}{2m}t} = (C_{1} + C_{2}t) e^{\frac{-k}{2m}t}, $

para $C_{1}$ e $C_{2}$ constantes que satisfarão as condições iniciais $y(0) = \theta_{0}$ e $y'(0) = v_{0}$.

Observe que ainda temos que a solução vai para zero quando $t \to \infty$. Também a solução passa uma única vez pela solução de equilíbrio, exatamente em

$\displaystyle t = -\frac{C_{1}}{C_{2}}, $

também para $C_{1}$ e $C_{2}$ com sinais contrários (pois $t \geq 0$).

Caso 3. Se $\Delta = (k^{2}L^{2}-4m^{2}Lg) < 0$ então as raízes da equação auxiliar são os números complexos conjugados

$\displaystyle x_{1} = \overline{x_{2}} = \frac{-k}{2m} + \frac{\sqrt{k^{2}L^{2}-4m^{2}Lg}}{2mL} i, $

e então a solução da equação diferencial (4.18) toma a forma (que mais nos interessa)

$\displaystyle \theta = \theta(t) = e^{\frac{-k}{2m}t} \left( C_{1} \cos(\omega t) + C_{2} {\mathrm {sen}}(\omega t) \right), $

com $\omega = \frac{\sqrt{k^{2}L^{2}-4m^{2}Lg}}{2mL}$ e $C_{1}$ e $C_{2}$ constantes que satisfazem as condições iniciais $y(0) = \theta_{0}$ e $y'(0) = v_{0}$.

Observe que agora temos um movimento oscilatório. Mesmo assim, a presença da exponencial com potência negativa nos diz que o movimento tende a zero quando $t \to \infty$. Porém agora o valor da constante de proporcionalidade é pequeno. Para ser mais preciso, $k < 2m\sqrt{\frac{g}{L}}$. Isto significa que a convergência para zero se dá de forma mais lenta, permitindo algum tempo de oscilação, antes do pêndulo parar. Esta parada ocorre na prática, mas teoricamente o pêndulo oscila para sempre com oscilação muito pequena.

Para finalizar esta seção observe que a equação (4.17) não foi utilizada até agora. Em verdade ela é útil para calcular a força de tração $T$, exercida pelo fio sobre o objeto, depois que tivermos determinado uma expressão para $\theta(t)$.

4.7 Sistema massa-mola

Vamos considerar que uma mola extensível, de comprimento $l$ em repouso, esteja presa verticalmente a um suporte rígido. Prendemos então um objeto de massa $m$ à extremidade livre da mola. Isto provocará uma distensão da mola, para um ponto de equilíbrio, por $s$ unidades de comprimento.

Parece natural que se deslocarmos a massa $m$ e a soltarmos, esta massa oscilará em movimento de sobe e desce. Queremos um modelo para determinar a sua posição com o tempo. Para equacionar o problema, fixemos um sistema coordenado (só precisaremos da componente vertical) cuja origem está no ponto que dista $L=(l+s)$ do suporte rígido e cresce no sentido do suporte.

Designemos $y(t)$ a posição do objeto no instante $t$, ou mais precisamente, a posição da extremidade da mola no instante $t$. Note então que a distância $d$ entre o objeto e o suporte rígido, no instante $t$ é

$\displaystyle d(t) = L - y(t). $

De acordo com o nosso referencial duas forças unidimensionais atuam sobre o objeto. A força peso $\vec{p}$ e a força de tração da mola $\vec{t}$, ambas com mesma direção (vertical) e sentidos contrários.

O peso $\vec{p}$, considerado negativo por estar em sentido contrário ao eixo fixado, é dado por $p = -mg$. A força de tração $\vec{t}$ é dada pela lei de Hooke. A lei de Hooke diz que a força de tração da mola é proporcional à distensão causada pela massa. Isto é, $t = ks$ sendo $k>0$ a constante de proporcionalidade, conhecida como constante de elasticidade da mola, que depende do material que a mola é composta.

Agora note que, como o sistema está em equilíbrio, a força resultante $\vec{F}$ é nula. Isto é, $\vec{F} = \vec{p} + \vec{t} = \vec{0}$, o que nos leva a

$\displaystyle ks-mg = 0. $

Desloquemos a massa por uma quantidade $y_{0}$ e deixamos o sistema livre para se movimentar. Agora a força de tensão $\vec{t}$ depende também da posição $y = y(t)$ do corpo. Temos assim,

$\displaystyle \vec{t} = k(s-y), $

pois a distenção da mola agora é $(s-y)$. De acordo com a segunda lei de Newton temos $\vec{F} = m\vec{a}$. Segue que

$\displaystyle m\vec{a} = \vec{F} = \vec{t} + \vec{p} = ks - ky - mg = -ky, $

e, portanto, a equação que descreve o movimento $y(t)$ do corpo é

$\displaystyle m\vec{a} = - ky. $

Como a aceleração $\vec{a}$ é a derivada segunda do movimento $y(t)$, então a equação diferencial

$\displaystyle y'' + \frac{k}{m} y = 0, $

modela o movimento da massa $m$ com o passar do tempo. Ainda temos as condições iniciais

$\displaystyle y(0) = y_{0}$   e$\displaystyle \quad y'(0) = v_{0} $

que siginificam respectivamente a posição inicial e a velocidade inicial (zero se o sistema é solto do repouso).

Temos então o Problema de Valor Inicial,

$\displaystyle \left\{ \begin{array}{l} y'' + \frac{k}{m} y = 0 \\ y(0) = y_{0}, \qquad y'(0) = v_{0} \end{array} \right.$ (4.19)

Esta equação diferencial é uma equação linear homogênea de ordem 2. Podemos verificar que a função dada por

$\displaystyle y = C_{1} \cos(\omega t) + C_{2} {\mathrm {sen}}(\omega t), $

com $\omega = \sqrt{\frac{k}{m}}$ e $C_{1}$ e $C_{2}$ são números reais quaisquer, é uma solução para a equação diferencial. Observe que o movimento é oscilatório em termos de senos e cossenos. As constantes $C_{1}$ e $C_{2}$ podem ser determinadas substituindo-se as duas condições $y(0) = y_{0}$ e $y'(0) = v_{0}$. Temos assim,

$\displaystyle \left\{ \begin{array}{l} y_{0} = y(0) = C_{1} \\ v_{0} = y'(0) = C_{2} \omega \end{array} \right. $

donde a solução é

$\displaystyle y = y_{0} \cos(\omega t) + \frac{v_{0}}{\omega} {\mathrm {sen}}(\omega t). $

Observe que para conhecer esta equação completamente ainda é necessário conhecer $\omega$ e, para isso, precisamos do valor da constante da mola $k$. Este valor pode ser determinado medindo-se o deslocamento $s$ causado pela massa $m$, pois como vimos $(ks-mg)=0$, ou ainda, $k = \frac{mg}{s} = \frac{p}{s}$, onde $p$ é o peso do objeto (o módulo da força peso $\vec{p}$).

Este modelo pode ser complicado um pouco mais. Para ser mais preciso, este modelo é muito simples, pois supõe condições que na prática são irreais. As únicas forças consideradas são a força peso e a força de tração da mola e isto supõe a ausência de outras forças externas, como por exemplo, a resitência do ar. Este modelo precisa então de vácuo perfeito. Por este motivo, o sistema acima é dito sistema do movimento livre não amortecido.

Um exemplo de complicação do problema é considerar que a mola “envelhece”. Em outras palavras, considerar que a constante $k$ da mola, seja variável com o tempo. Fisicamente isto significa que a mola perde suas propriedades iniciais de deformação com o passar do tempo.

Poderíamos considerar a função de elasticidade da mola seja dada por $ke^{-\alpha t}$ com $k>0$ e $\alpha > 0$. Temos então uma equação diferencial dada por $y'' + \frac{k}{m}e^{-\alpha t}y = 0$. Outra função de elasticidade da mola que poderíamos considerar é $k\frac{1}{t}$ para $k>0$ e então a equação diferencial se torna $y'' + \frac{k}{mt}y = 0$. Em ambos os casos temos equações diferenciais de ordem 2 com coeficientes variáveis e isto dificulta muito a obtenção de uma solução analítica.

Outra complicação que podemos causar, que não dificulta determinar uma solução, é considerar que o corpo oscile imerso em algum fluido, como ar, água, óleo, entre outros. Isto obrigará a consideração de alguma força externa de atrito agindo sobre o sistema.

Em geral, uma força de atrito é considerada como sendo proporcional a uma potência da velocidade. Como a velocidade de oscilação da massa é relativamente pequena, em geral a potência considerada é 1, isto é, a força de atrito $\vec{r}$ é proporcional à velocidade $\vec{v}$.

Nestes termos, consideremos

$\displaystyle \vec{r} = -\lambda \vec{v}, $

para $\lambda > 0$. O sinal negativo é decorrência de que a força de amortecimento é contrária à velocidade. Assim, a força resultante $\vec{F}$ é

$\displaystyle \vec{F} = \vec{p} + \vec{t} + \vec{r}, $

e temos

$\displaystyle m\vec{a} = \vec{F} = \vec{t} + \vec{p} + \vec{r} = ks - ky - mg - \lambda \vec{v} = - ky - \lambda \vec{v}. $

Lembrando que a aceleração é a derivada segunda da posição ( $\vec{a} = y''$) e que a velocidade é a derivada primeira da posição ( $\vec{v} = y'$), então vem a equação diferencial

$\displaystyle my'' + \lambda y' + ky = 0,$ (4.20)

sujeita às condições iniciais $y(0) = y_{0}$ (posição inicial) e $y'(0) = v_{0}$ (velocidade inicial).

A solução desta equação agora depende agora das raízes da equação auxiliar quadrática,

$\displaystyle mx^{2} + \lambda x + k = 0, $

e, portanto, do comportamento de $\Delta = \lambda^{2} - 4mk$. Temos três casos a considerar.

Caso 1. Se $\Delta = (\lambda^{2} - 4mk) > 0$ então podemos verificar que a função dada por

$\displaystyle y(t) = C_{1} e^{x_{1} t} + C_{2} e^{x_{2} t}, $

com

$\displaystyle x_{1} = \frac{-\lambda + \sqrt{\lambda^{2}-4mk}}{2m},$   e$\displaystyle \qquad x_{2} = \frac{-\lambda - \sqrt{\lambda^{2}-4mk}}{2m}, $

é solução da equação diferencial (4.20) para quaisquer constantes reais $C_{1}$ e $C_{2}$.

Observe que

$\displaystyle x_{1}$ $\displaystyle = \frac{-\lambda + \sqrt{\lambda^{2}-4mk}}{2m} < \frac{-\lambda + \sqrt{\lambda^{2}}}{2m} = 0,$    
$\displaystyle x_{2}$ $\displaystyle = \frac{-\lambda - \sqrt{\lambda^{2}-4mk}}{2m} < 0,$    

e isto garante que, independentemente das constantes $C_{1}$ e $C_{2}$, ou da posição inicial e da velocidade inicial, a solução do sistema tende a zero exponencialmente quando $t \to \infty$. De outra forma,

$\displaystyle \lim_{t \to \infty} y(t) = 0. $

Isto significa que o movimento do corpo tende a cessar exponencialmente. É uma consequência imediata de uma constante de amortecimento $\lambda$ muito grande. Grande o suficiente para garantir que $\lambda^{2} - 4mk > 0$. Neste caso dizemos que o sistema é super amortecido.

Caso 2. Se $\Delta = (\lambda^{2}-4mk) = 0$ então podemos verificar que a função

$\displaystyle y(t) = C_{1} e^{x t} + C_{2}te^{x t}, $

é solução da equação diferencial (4.20) para $C_{1}$ e $C_{2}$ constantes reais e $x = -\frac{\lambda}{2m}$ a única raiz real da equação auxiliar.

Note que ainda temos $x < 0$ e, portanto, a solução ainda decai (exponencialmente) para zero quando $t \to \infty$. Este sistema é dito criticamente amortecido, pois ainda é amortecido, mas qualquer decréscimo na constante de amortecimento $\lambda$, o movimento se tornará oscilatório.

Caso 3. Se $\Delta = (\lambda^{2}-4mk) < 0$ então temos que a função

$\displaystyle y(t) = e^{\frac{-\lambda}{2m}t} \left( C_{1}\cos(\omega t) + C_{2} {\mathrm {sen}}(\omega t) \right), $

com $\omega = \frac{\sqrt{4mk-\lambda^{2}}}{2m}$, é solução da equação diferencial (4.20) para $C_{1}$ e $C_{2}$ constantes reais quaisquer. Observe que mesmo sendo um movimento oscilatório, o termo $e^{\frac{-\lambda}{2m}t}$ tende a zero quando $t \to \infty$. Isto significa que este movimento oscilatório ainda tende a diminuir e cessar com o tempo. Porém isto ocorrerá de forma mais lenta permitindo algum tempo de oscilação do corpo antes da parada.

Este tempo de oscilação naturalmente depende de $\lambda$ que é a constante de proporcionalidade da força de atrito. Quanto menor o valor de $\lambda$ mais tempo de oscilação antes de o corpo parar. Esta parada ocorre na prática, mas lembremos que teoricamente a oscilação ocorre para todo $t \geq 0$.